Chapter 6 Raster processing

Last updated: 2020-08-12 00:36:05

Aims

Our aims in this chapter are:

  • Get raster subsets
  • Set raster metadata and dimension properties
  • Calculate new rasters based on one or more overlapping rasters, using raster algebra

We will use the following R packages:

  • stars

6.1 Time series for single pixel

6.1.1 Selecting pixel by row & column

In most of the examples in this Chapter, we are going to use the MOD13A3_2000_2019.tif raster which we already met in Section 5.3. Let’s read it into memory:

Keep in mind this is a raster time series, where the “layers” refer to NDVI images taken in different times. As an exercise of accessing raster values (Section 5.3.8.4) and working with time series (Section 3.1.3), in this Section we are going to extract and plot a NDVI time series for a single pixel.

In Section 5.3.8.2, we saw how the matrix or array of raster values can be accessed using the [[ operator, as in r[[1]]. As another exercise, let’s access a “slice” of a single pixel through all of the raster layers, as follows:

The result is a vector (why?). Plotting the vector displays a time-series of NDVI at a particular location (Figure 6.1):

Single pixel values across all layers

Figure 6.1: Single pixel values across all layers

6.1.2 Combining values with dates

The file MOD13A3_2000_2019_dates2.csv corresponds to the third dimension of MOD13A3_2000_2019.tif, containing the dates when each NDVI image was captured. This file includes the additional season column which we calculated in Section 4.6.

Using the MOD13A3_2000_2019_dates2.csv table, we can display dates on the x-axis (Figure 6.2). First we read the dates table:

The we can plot the dates on the x-axis, as follows:

Single pixel values across all layers

Figure 6.2: Single pixel values across all layers

6.1.3 Visualizing seasonal pattern

Figure 6.2 clearly shows the seasonal pattern of NDVI. However, we can further improve the interpretability of the time series plot if we mark seasons with different color. One way to do that is to add the NDVI observations of each season separately to the plot using a for loop.

As a first step, we define the vector of seasons (seasons) and the corresponding vector of colors (cols):

Then, we can use a for loop (Section 4.2.3) to mark the portion of the NDVI time series from each season (Figure 6.3):

Single pixel values across all layers

Figure 6.3: Single pixel values across all layers

6.2 Raster subsetting

6.2.1 Selecting rows, column and layers

We can get a subset of a stars object while keeping all of its properties, using the [ operator.

The stars subset operator [ works as follows:

  • The first index selects attributes
  • The second index selects the first dimension, usually [x], i.e., raster columns
  • The third index selects the second dimension, usually [y], i.e., raster rows
  • The following indices select the remaining dimensions, if any

Again, keep in mind that the order of stars indices is opposite of the order we are used to in R, since the first dimension refers to columns [x], while the second dimension refers to rows [y].

For example, the following expression creates a subset with two columns, three rows and two layers from r:

The raster subset is plotted in Figure 6.4:

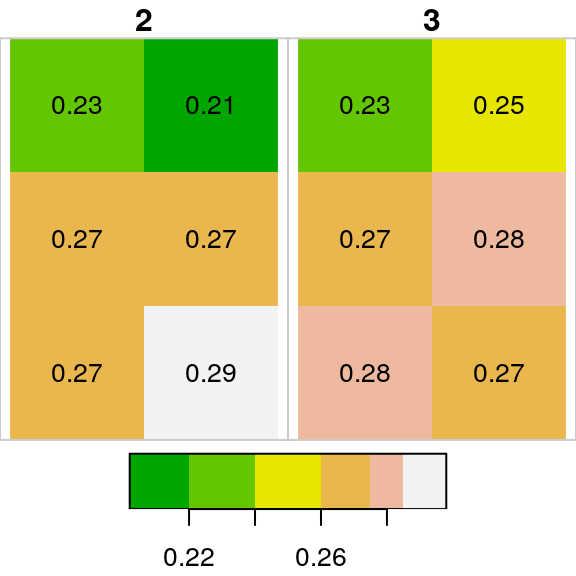
Raster subset

Figure 6.4: Raster subset

What is the meaning of the following plot (Figure 6.5)?

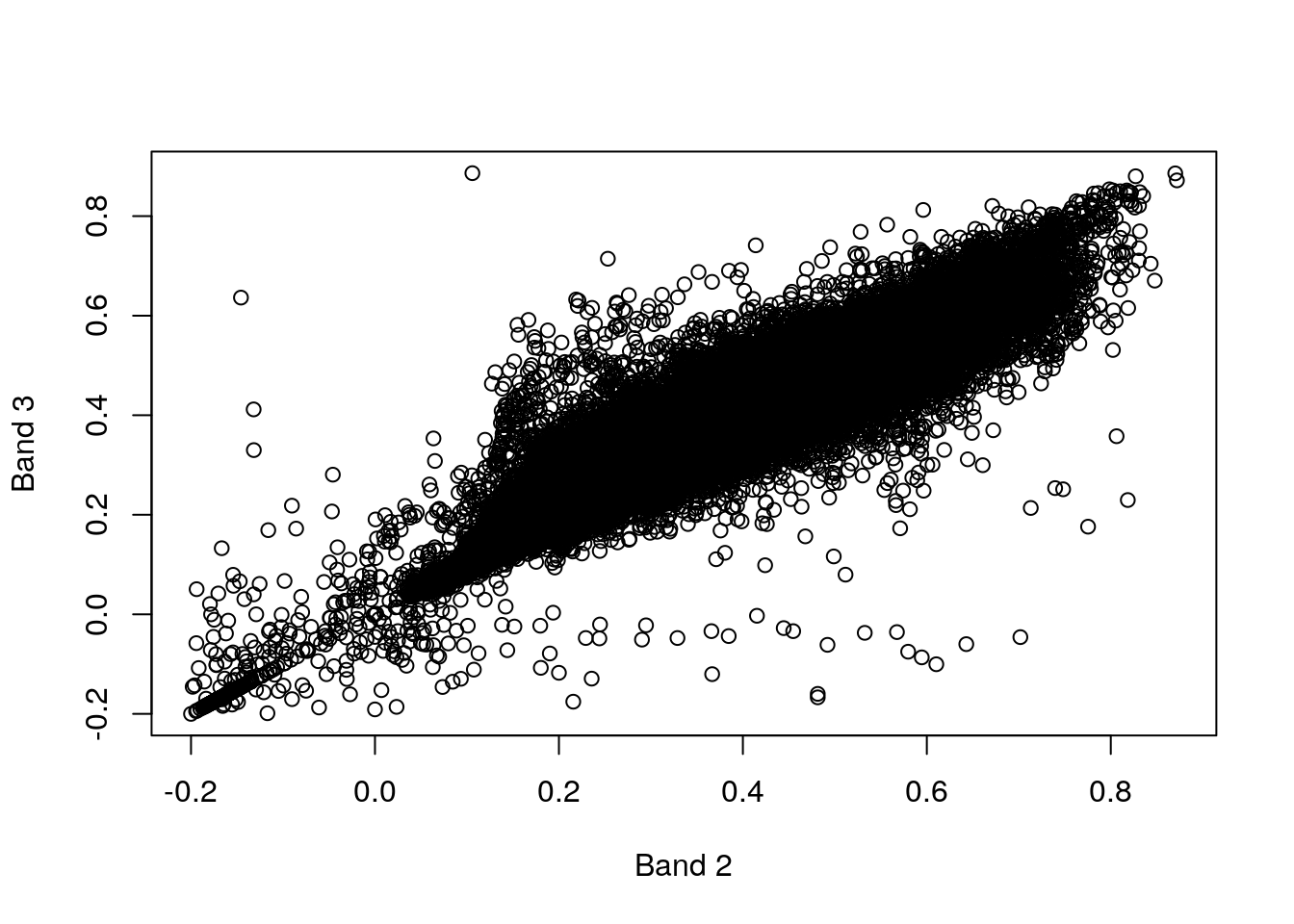
Band 3 as function of band 2

Figure 6.5: Band 3 as function of band 2

6.2.2 Index normalization

The st_normalize function can be used to “reset” the indices of the subset, i.e., the from and two dimension properties (Section 6.3.1) so that they start from 1 once again. For example:

Normalizing the indices is necessary for the raster to be processed by some of the functions in the stars package, as we will see later on.

6.2.3 Dropping unnecessary dimensions

When a subset includes just one step along one or more dimensions, the “unnecessary” demensions can be dropped using drop=TRUE. For example, compare the output of the following two expressions. Both expressions return a subset consisting of the 7th layer of r. However, the first expression returns a three-dimensional stars object (with a single layer in the 3rd dimension), while the second expression returns a two-dimensional stars object where the 3rd dimension was “dropped”:

Accordingly, the raster values are represented as an array in the first case, and as a matrix in the second case:

6.3 Raster dimensions

6.3.1 Getting dimension properties

As mentioned in Section 5.3.8.3, the st_dimensions function can be used to access dimension properties of a stars object. The function resurns an object of class dimensions. Printing the object gives a nice summary of the raster dimensions and their properties:

Internally, the dimensions object is a list of dimensions (one element per dimension). Each element is also a list, with the elements being the various properties of a single dimension:

Individual dimensions can be accessed using the $ operator by list element name, or the [[ operator by list element index or name (more on lists in Section 11.1). For example, all following there expressions give the same result, the properties of the 1st dimension "x":

Properties of individual dimensions can be accessed through further subsetting (Figure 6.6). For example, the following expression returns the offset and delta (resolution) properties of the "x" dimension:

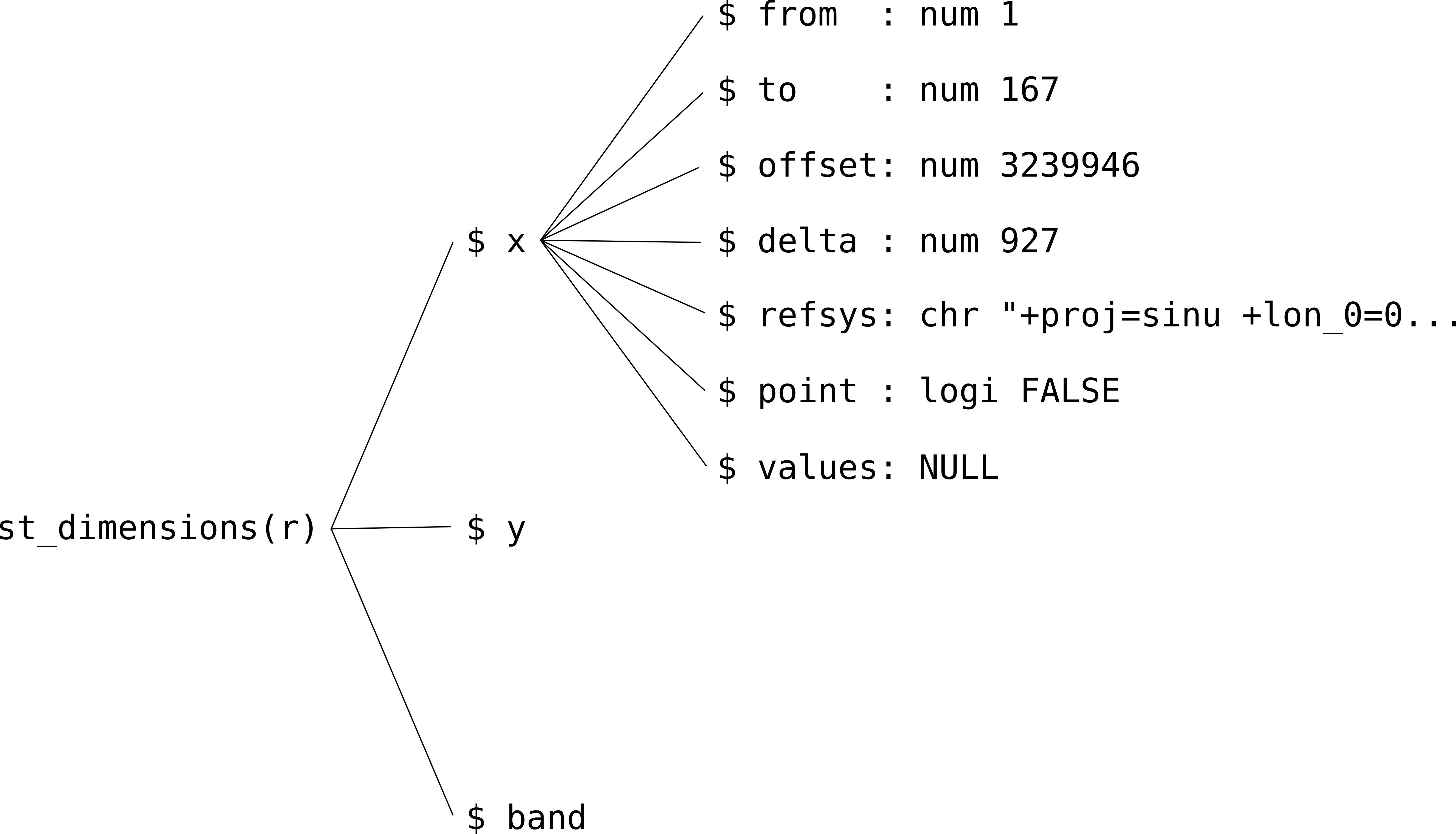
The hierarchical structure of `stars` dimensions properties

Figure 6.6: The hierarchical structure of stars dimensions properties

The meaning of the seven properties that every stars dimension has is summarized in Table 6.1.

Table 6.1: Dimension properties in a stars object
Dimension Class Meaning
from numeric length 1 The start index
to numeric length 1 The end index
offset numeric length 1 The start coordinate (or time) of the first element (i.e., the pixel/cell boundary)
delta numeric length 1 The increment / cell size (i.e., resolution)
refsys character, or crs The Coordinate Reference System (CRS)
point logical length 1 Whether cells/pixels refer to areas/periods, or to points/instances (may be NA)
values NULL, or an object that gives the specific dimension values The dimension values

For more information on stars dimensions, see the official stars Data Model article.

6.3.2 Setting dimension properties

A .tif file cannot hold metadata regarding raster “layers”, such as the date when the images were captured in case the layers comprise a time series. Indeed, the third dimension of r does not contain any information other than the start and end indices (1 and 233):

We can incorporate more information into a stars object on our own. This is done using function st_set_dimensions, where we need to specify:

  • .x—The stars object
  • which—The index or name of the dimension to be modified

as well as dimension properties and their new values, such as:

  • names—The dimension name(s)
  • values—The values along the dimension
  • offset—The offset
  • delta—The delta (i.e., resolution)

For example, for a non-spatial dimension that represents time, such as the "band" dimension in r, we can set the values (the dates or times) and the dimension name as follows:

Now, the 3rd dimension of r contains the Date values:

If necessary, the dimension values can be accessed directly using st_get_dimension_values. For example:

What is the meaning of the dimension values given by st_get_dimension_values(r, 1) and st_get_dimension_values(r, 2)? Given that st_dimensions(r)[[1]]$values and st_dimensions(r)[[2]]$values are NULL, where do you think these dimension values come from?

Why do we need to bother with editing or supplementing dimension properties? One reason is that it is more convenient to have all of the relevant raster data in the same object (rather than two separate objects, such as r and dates). Moreover, adding descriptive information of stars dimensions is useful in various contexts. For example, the values apprear in plot output (Figure 6.7):

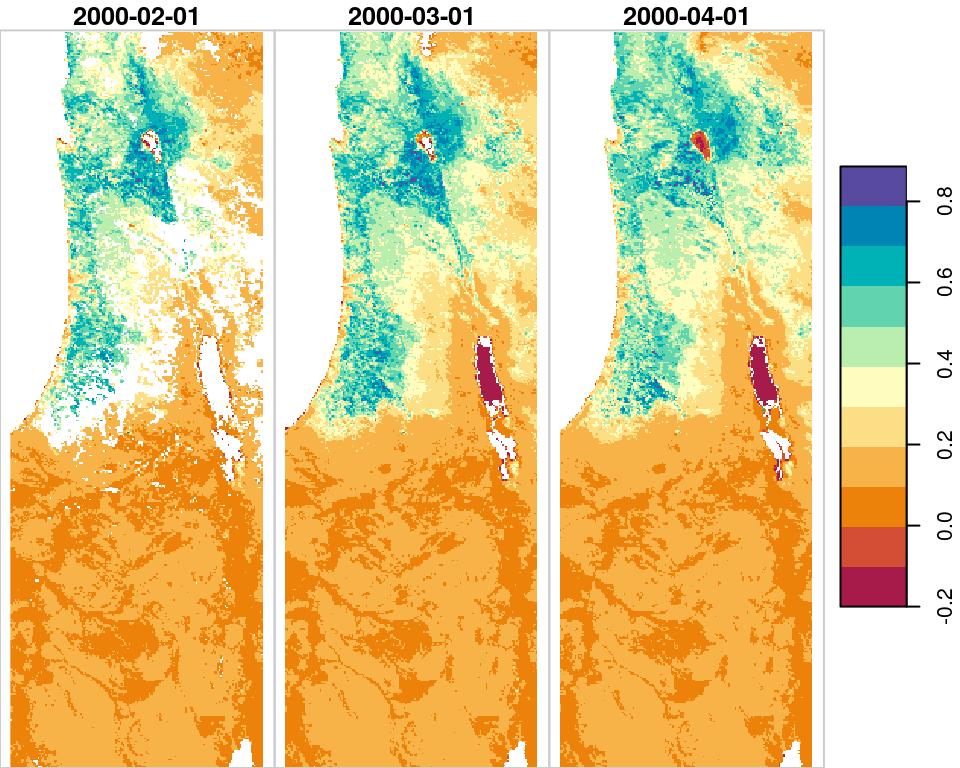
Date lables for raster layers, i.e., the third raster dimension

Figure 6.7: Date lables for raster layers, i.e., the third raster dimension

and are kept when converting the raster to a data.frame:

6.3.3 Converting a matrix to raster

6.3.3.1 The volcano matrix

Converting a matrix to a stars raster is rarely needed in practice, since most of the time you will be working with existing rasters imported from files (Section 5.3.2). However, experimenting with the matrix→stars conversion will help us better understand the nature of rasters in general and the stars class in particular.

When converting a matrix or an array to a stars raster, we must manually set the properties of the dimensions, most importantly the spatial dimensions "x" and "y".

In the first example, we will convert the built-in volcano matrix (Section 5.1.6) to a stars raster. First, we convert the transposed (why?) matrix to a stars raster:

Then, we may want to set the dimension and attribute names:

Finally, we set the offset and delta of the x and y dimensions, or, other words, where do these axes start from and what is their step size (i.e., resolution). The offset values of 0 (see below), in this case, is arbitrary. The delta is also arbitrary, but should be equal for both x and y (unless we want to have asymmetrical pixels). In this case, according to the ?volcano help page, the matrix represents a 10m by 10m grid, so we will use a delta of 10 or -10 so that the coordinate units are “meters”. The delta of the y-axis is negative (!), so that the the values decrease when going to from 1st row to last:

Compare the output of plot(v, axes=TRUE) before and after setting the offset and delta to see the effect of those settings.

The result is shown in Figure 6.8. Note that we need to use the reset=FALSE argument whenever we want to have additional layers, such as a contours, in a stars plot:

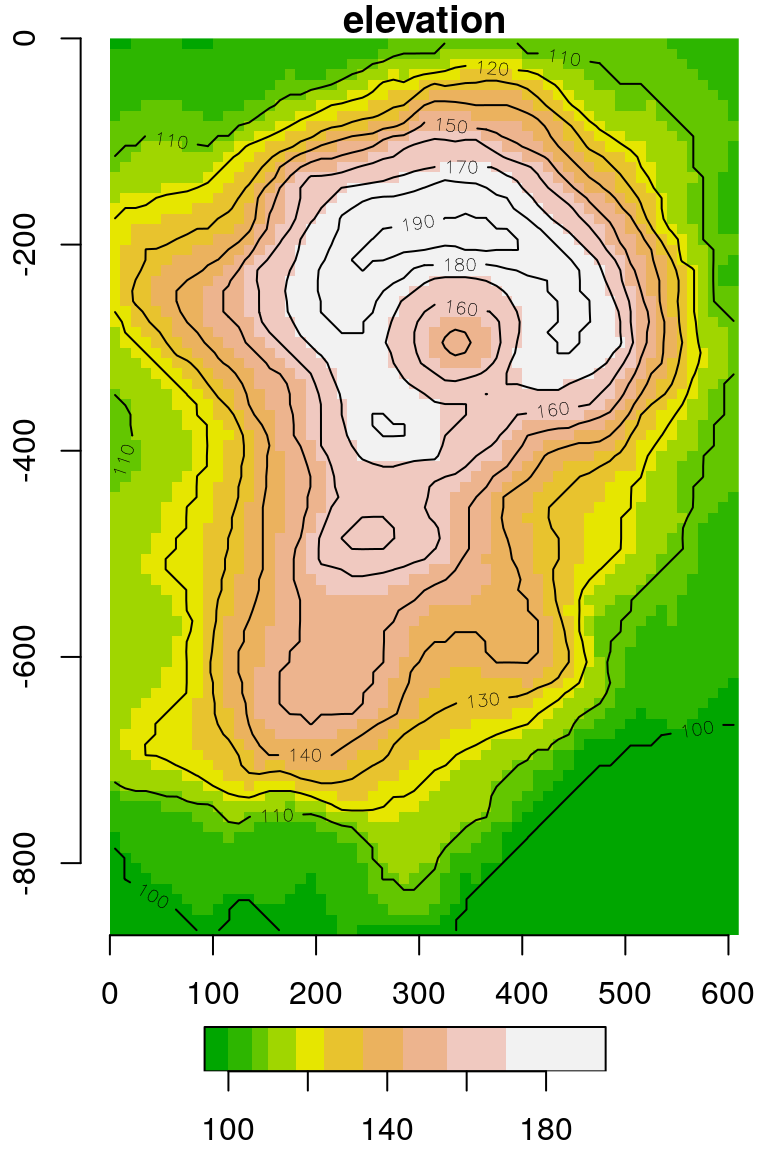
The `volcano` matrix converted to `stars` raster

Figure 6.8: The volcano matrix converted to stars raster

The fact that the offset is arbitrary is demonstrated with the following expression, which “shifts” the raster so that the (0, 0) coordinate is in the botton-left rather than top-left corner:

The modified volcano raster is shown in Figure 6.9.

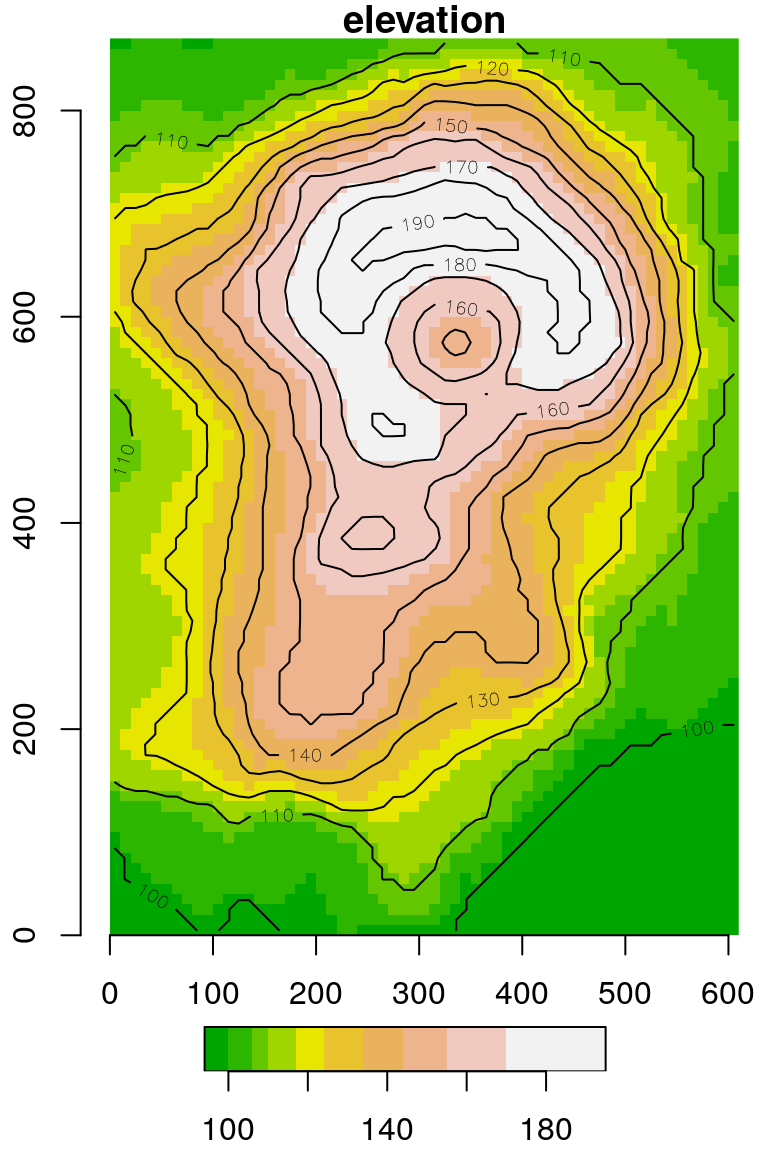
The `volcano` raster with modified offset

Figure 6.9: The volcano raster with modified offset

Comparing Figures 6.8 and 6.9, the only thing that has changed are the y-axis coordinates.

6.3.3.2 The Haifa DEM matrix

In the second example, we will recreate the dem.tif small DEM of Haifa using a matrix with its values. Here is the matrix we start with:

This time, assuming we know the right spatial reference information, we can create a truly georeferenced stars object. To position a matrix or array in geographic space (Section 5.3.1), we need to know the coordinates of the starting point (offset) and the resolution (delta) for the "x" and "y" dimensions, and the CRS.

For example, the following code section sets the two offset values (679624 and 3644759), the resolution (2880) and the CRS (32636). Note that the CRS is specified using st_set_crs and an EPSG code. Again, the y-axis resolution is negative, so that going down the matrix rows translates to decreasing y-axis values.

The result is identical to dem.tif (Figure 5.15), as shown in Figure 6.10:

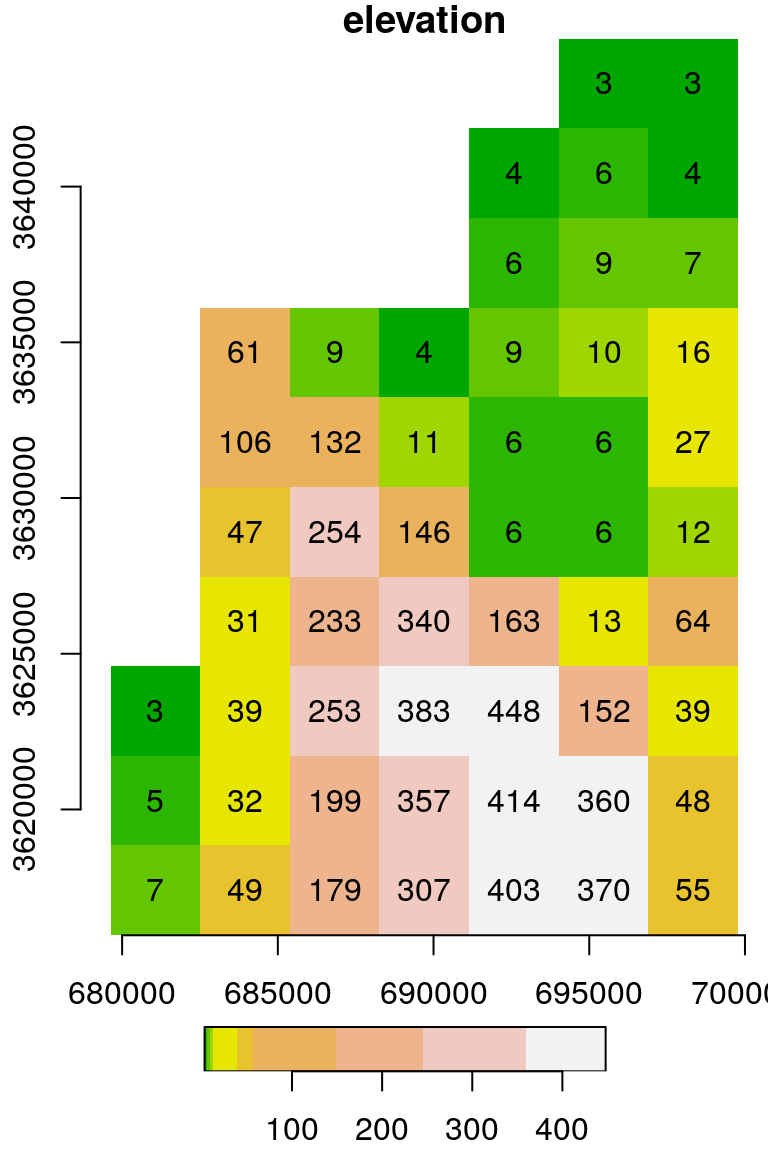
`matrix` converted to a `stars` object: Digital Elevation Model (DEM) of haifa

Figure 6.10: matrix converted to a stars object: Digital Elevation Model (DEM) of haifa

The effect of transposing the input matrix and modifying the sign of the y-axis delta is summarized in Figure 6.11. As we can see from this image, when delta_y is negative (while delta_x is positive), a transposed raster layer matrix, i.e., t(r[[1]]), matches the “true” spatial arrangement of the raster values. This is the most common scenario and the only one we will encounter in this book.

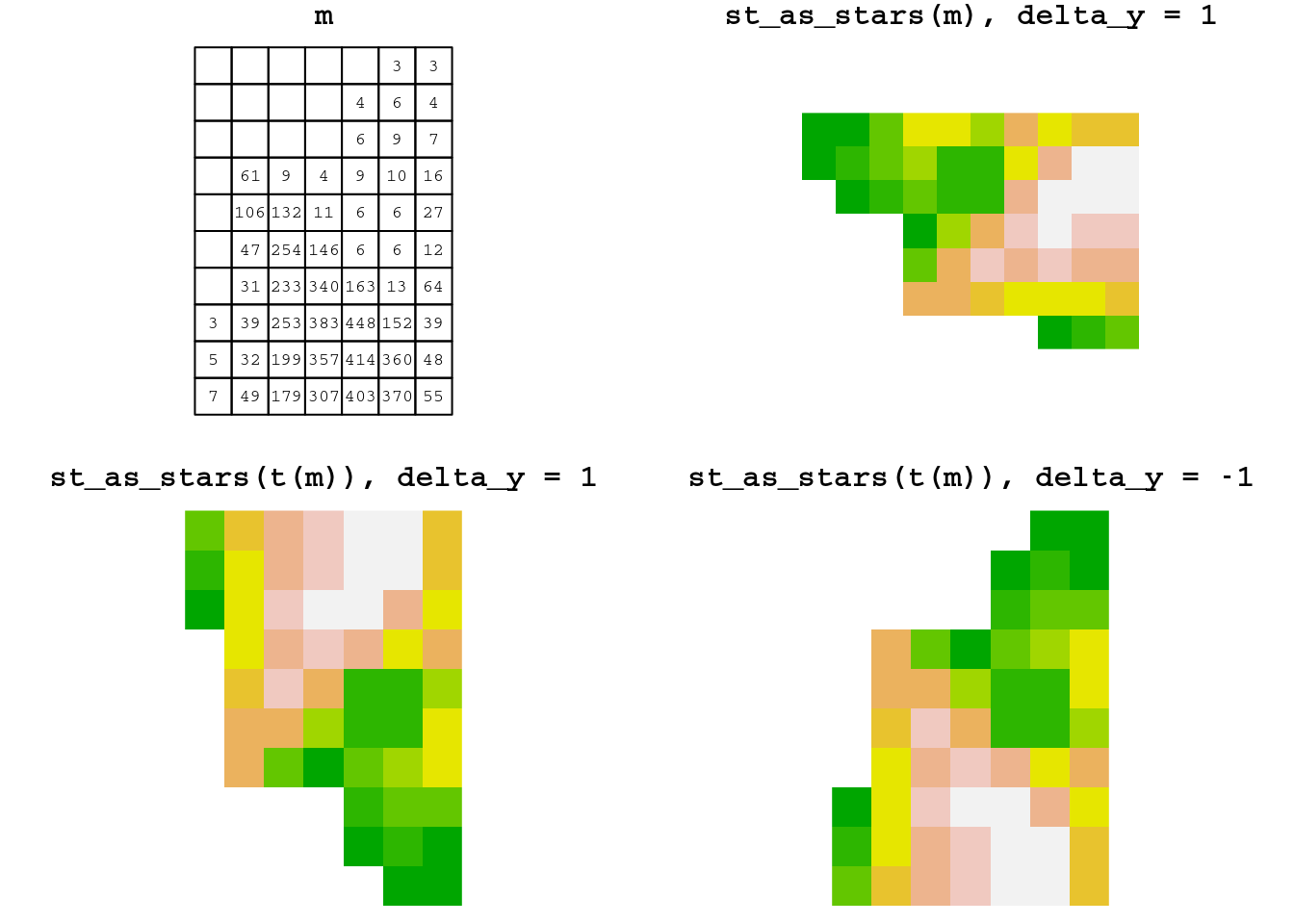
Converting `matrix` to `stars`: the effect of transposing the input matrix and modifying the sign of the y-axis delta

Figure 6.11: Converting matrix to stars: the effect of transposing the input matrix and modifying the sign of the y-axis delta

6.4 Raster algebra

6.4.1 Arithmetic and logical operations on layers

Often we have one or more overlapping rasters, and we want to apply the same operation on all pairs, triplets, etc., of overlapping pixels (Figure 6.12). This is known as raster algebra.

Raster algebra^[http://rpubs.com/etiennebr/visualraster]

Figure 6.12: Raster algebra26

In raster algebra, we can use arithmetic and logical operators to make calculations:

  • Arithmetic: +, -, *, /
  • Logical: <, <=, >, >=, ==, !=, !

on each pair of overlapping rasters, to get a new raster where each pixel value is the result of the given operation on the overlapping pixels in the input rasters. The operations can also combine rasters and numeric values, in which case the numeric value is recycled.

We can also use functions such as:

  • Functions: abs, round, ceiling, floor, sqrt, log, log10, exp, cos, sin

which are applied on an individual raster, transforming each of its pixel, separately.

For the next few examples, let’s create two single-band rasters named x and y. Note that we are using round to transform each of the rasters to rounded values with two decimal places:

Figure 6.13 shows the two rasters x and y:

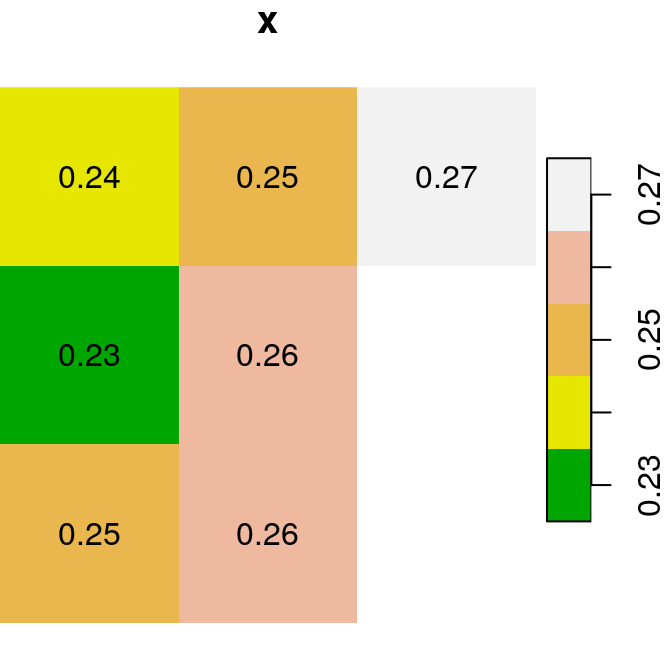
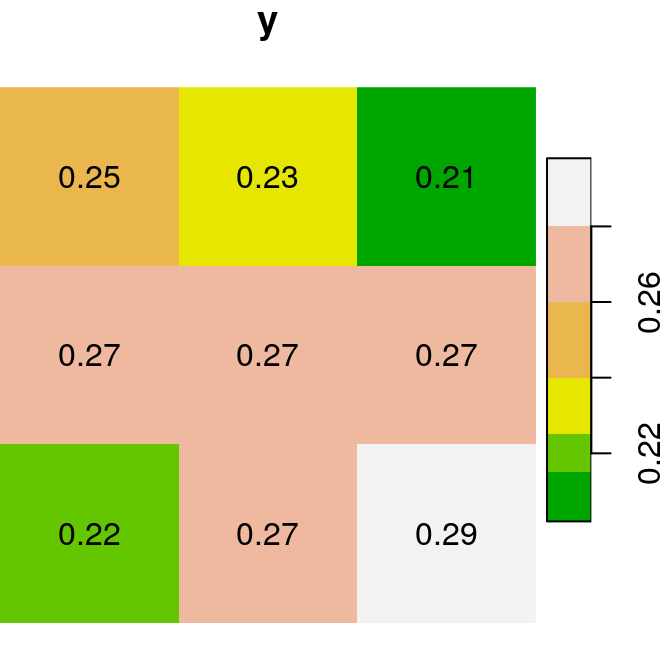
Two small `stars` rasters `x` and `y` to demonstrate raster algebraTwo small `stars` rasters `x` and `y` to demonstrate raster algebra

Figure 6.13: Two small stars rasters x and y to demonstrate raster algebra

As a first example of raster algebra, we calculate x+y, where each pixel value is the sum of two corresponding pixels in x and y (Figure 6.14):

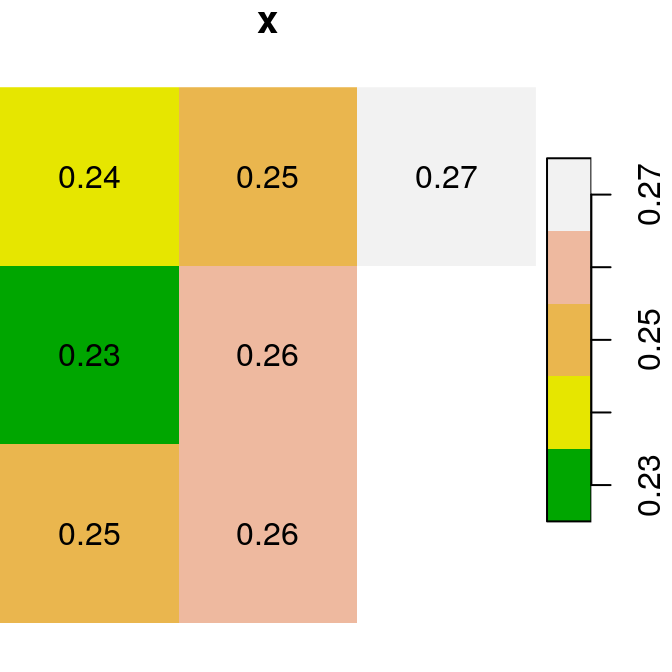
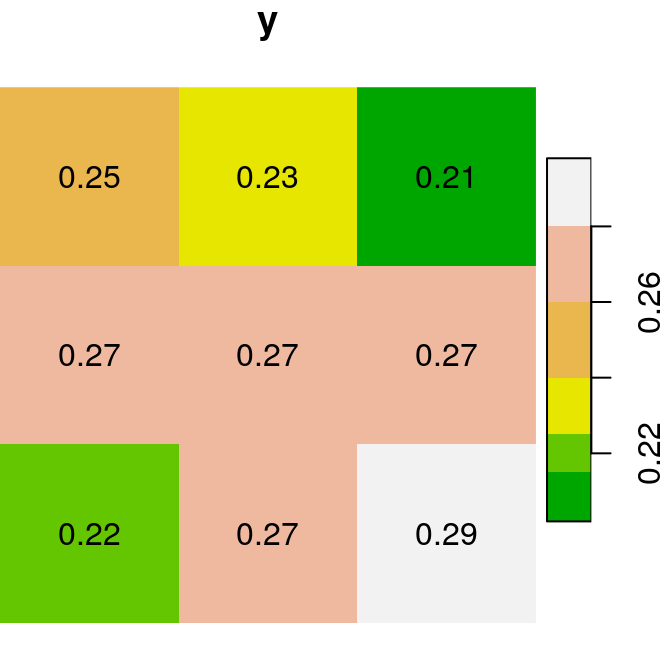
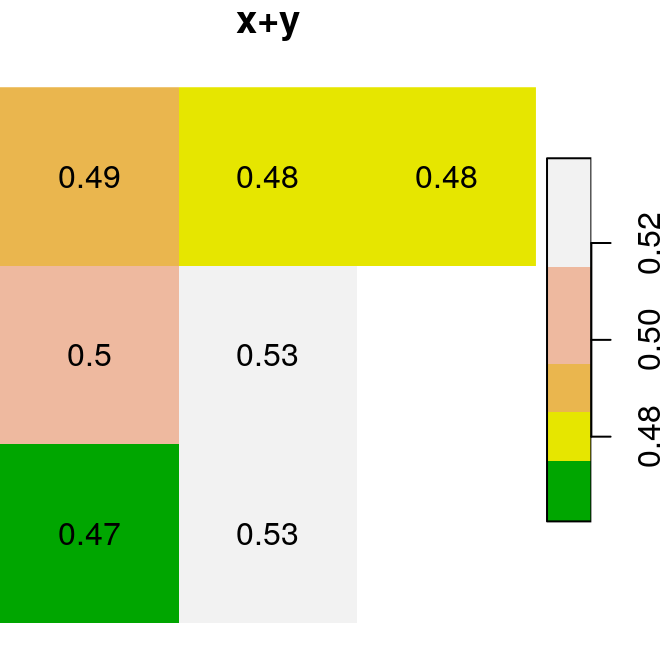
`x`, `y` and `x+y``x`, `y` and `x+y``x`, `y` and `x+y`

Figure 6.14: x, y and x+y

Here are several other examples of raster algebra: x-y, x*y and x+5. Note that x+5 combines a raster and a numeric value, rather than two rasters, in which case the numeric value is recycled (Figure 6.15):

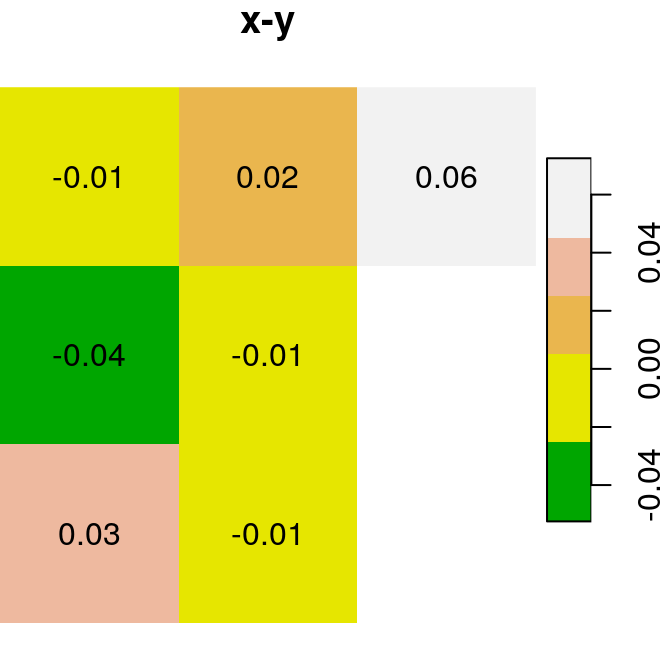
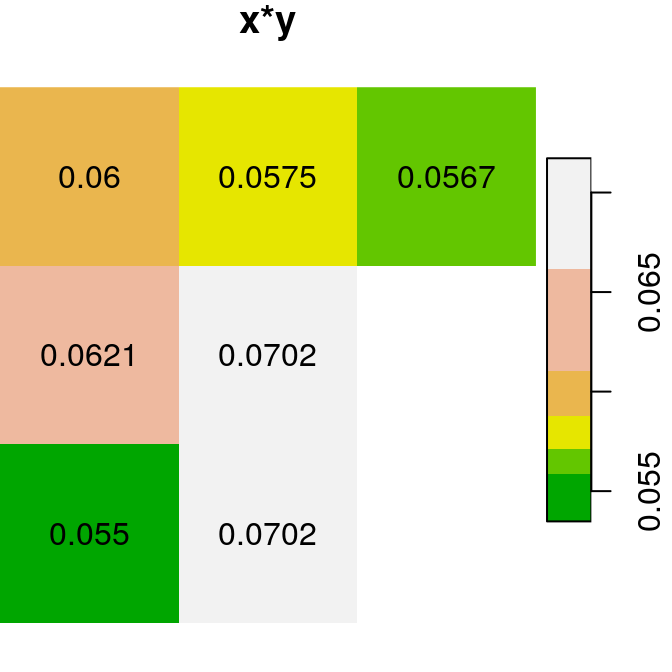
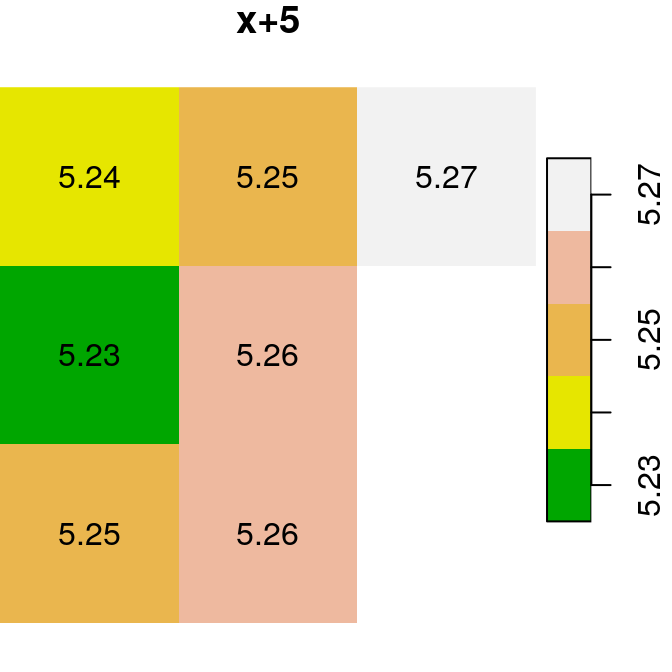
`x`, `y` and `x+y``x`, `y` and `x+y``x`, `y` and `x+y`

Figure 6.15: x, y and x+y

A logical raster algebra operation produces a logical raster, a raster where pixel values are TRUE or FALSE (or NA). For example, Figure 6.16 shows the logical rasters x>0.25, x<y and is.na(x):

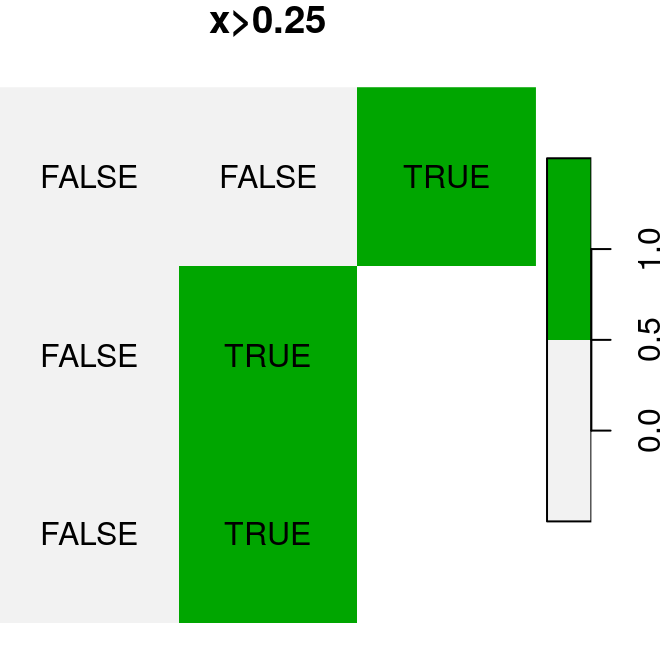
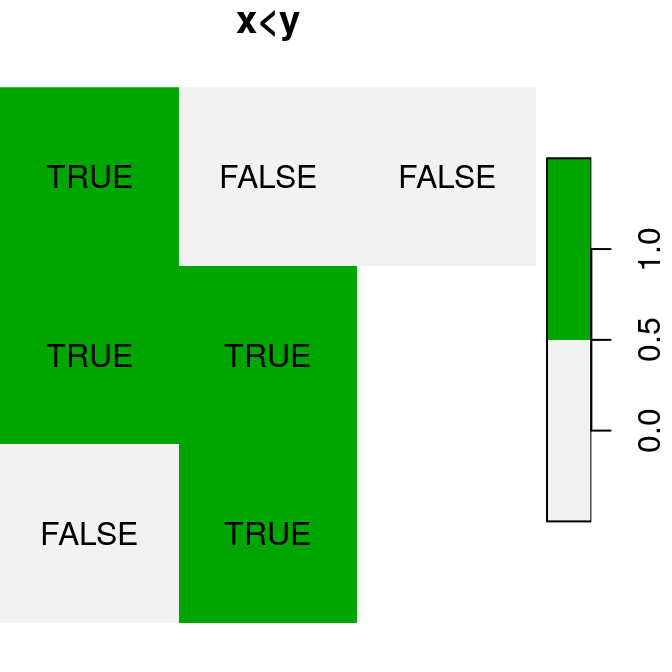
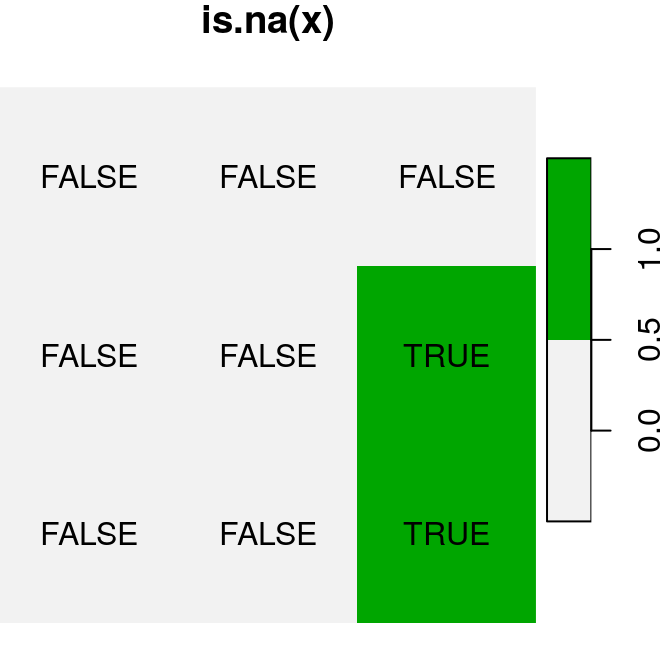
Logical raster algebra operations: `x>0.25`, `x<y` and `is.na(x)`Logical raster algebra operations: `x>0.25`, `x<y` and `is.na(x)`Logical raster algebra operations: `x>0.25`, `x<y` and `is.na(x)`

Figure 6.16: Logical raster algebra operations: x>0.25, x<y and is.na(x)

In operations where a numeric representation is required, such as:

  • An arithmetic operation
  • Saving to a file

logical raster values TRUE and FALSE automatically become 1 and 0, respectively. For example (Figure 6.17):

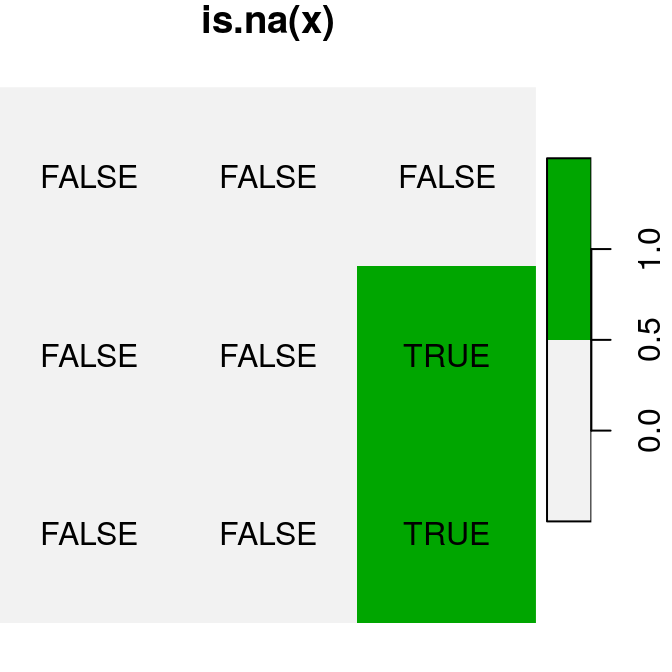
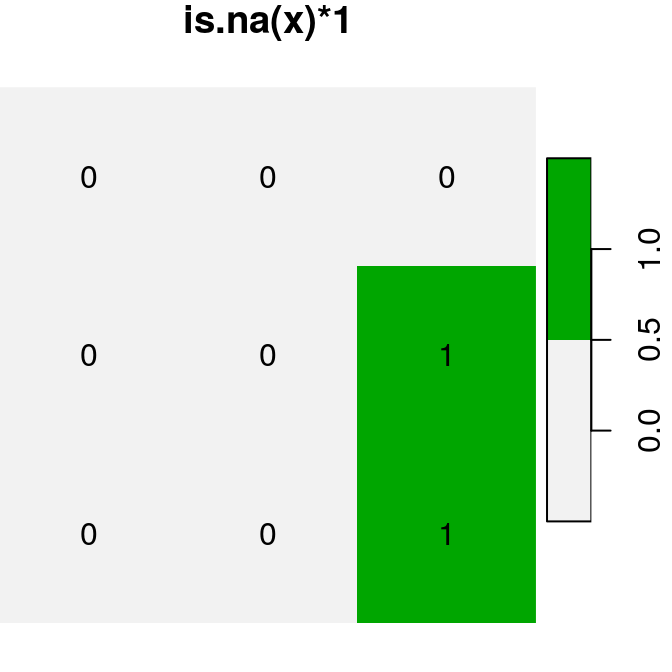
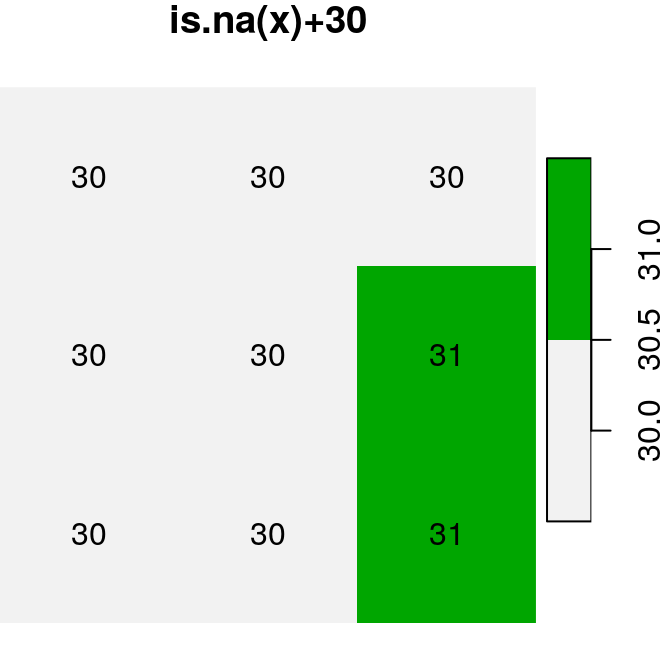
Conversion of raster values from `logical` to `numeric`Conversion of raster values from `logical` to `numeric`Conversion of raster values from `logical` to `numeric`

Figure 6.17: Conversion of raster values from logical to numeric

A logical raster can be used to assign new values into a subset of raster values. For example, we can use the logical raster is.na(r) to replace all NA values in the raster r with a new value:

The “before” and “after” images are shown in Figure 6.18:

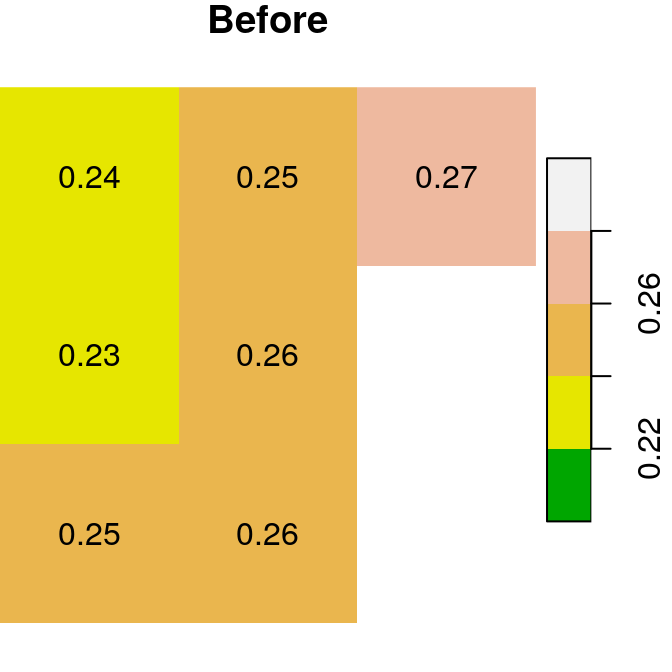
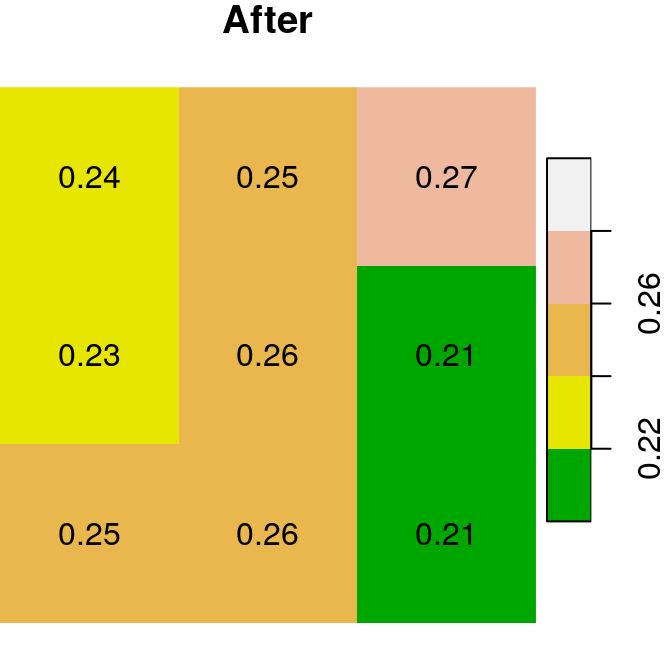
Assignmnent to raster subset using logical raster (before and after)Assignmnent to raster subset using logical raster (before and after)

Figure 6.18: Assignmnent to raster subset using logical raster (before and after)

How can we replace the NA values in x with the average of all non-missing values?

How can we calculate the proportion of NA values in x?

6.4.2 Landsat image

For the following example, let’s read another multi-band raster file named landsat_04_10_2000.tif. This is a part of a Landsat-5 satellite image with bands 1-5 and 7, after radiometric and atmospheric corrections. The raster values represent spectral reflectance, therefore all values are between 0 and 1.

We can assign meaningful layer names according to the spectral range that is captured by each band27:

Protting the raster shows the reflectance images for each spectral band (Figure 6.19):

Landsat satellite image, bands 1-5 and 7

Figure 6.19: Landsat satellite image, bands 1-5 and 7

6.4.3 True color and false color images

An RGB image is an image where the colors are defines based on red, green, and blue intensity per pixel. An RGB image can therefore be constructed from red, green, and blue bands in a multispectral sensor (Figure 6.20), such as the ones in a digital camera or a satellite.

RGB image^[https://datacarpentry.org/organization-geospatial/01-spatial-data-structures-formats/index.html]

Figure 6.20: RGB image28

A true color image is an image where the red, green and blue reflectance are red, green and blue colors. A true color image thus simulates the way that we would see the photographed area when looking from above, with the human eye. A false color image is an image where colors are mapped in any different way. A false color image can also include spectral bands that the human eye connot see, such as Near Infra Red (NIR).

True color and false color images can be produced with the plot function, specifying the red, green and blue bands with the rgb parameter. For example, in the Landsat image l, red, green and blue bands are 3, 2 and 1, therefore specifying rgb=c(3,2,1) produces a true color image (Figure 6.21). A different designation, rgb=c(4,3,2), produces a commonly used false color image where NIR is mapped to red, red is mapped to green and green is mapped to blue29 (Figure 6.21):

True color (left) and false color (right) imagesTrue color (left) and false color (right) images

Figure 6.21: True color (left) and false color (right) images

6.4.4 Calculating NDVI

NDVI is defined as the difference between NIR and Red reflectance, divided by their sum:

\[NDVI=\frac{NIR-Red}{NIR + Red}\]

We can calculate an NDVI image based on the red and NIR bands in the Landsat image l, using raster algebra:

The resulting NDVI image is shown in Figure 6.22:

An NDVI image calculated based on a Landsat satellite image

Figure 6.22: An NDVI image calculated based on a Landsat satellite image

To get another perspective on the spatial pattern of NDVI, we can use equal breaks and a more diverse color scale. The hcl.colors function offers numerous color scales useful for mapping. For example, the following expression returns 11 colors from the "Spectral" color scale:

The colors can then be passed to the col parameter in plot (Figure 6.23):

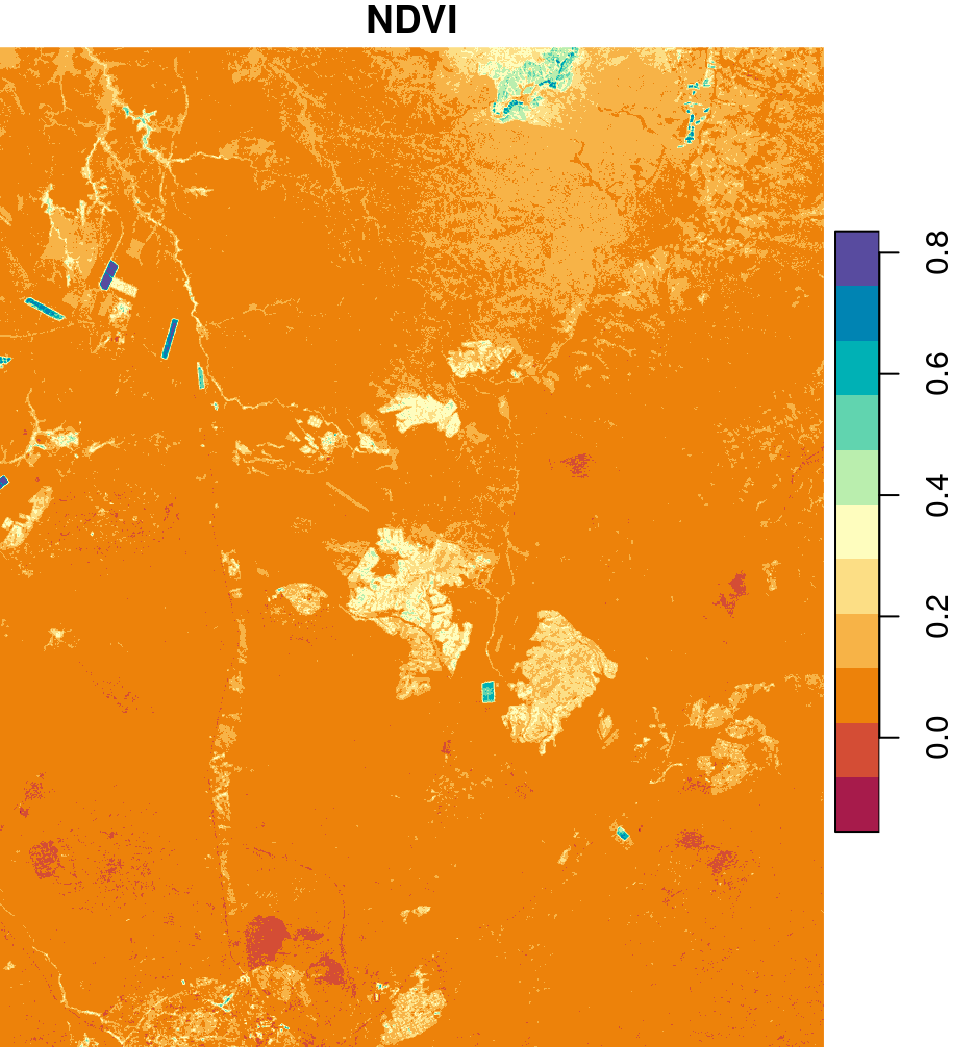
An NDVI image using the `"Spectral"` color scale

Figure 6.23: An NDVI image using the "Spectral" color scale

6.5 Classification

Raster classification is the process of converting a continuous raster to a discrete one, by giving all pixels in a particular range of values a new uniform value (Figure 6.24).

Raster classification^[http://rpubs.com/etiennebr/visualraster]

Figure 6.24: Raster classification30

A raster can be reclassified, i.e., converted from a continuous raster to a categorical one, by assigning a new value to distinct ranges of the original values. For example, we can reclassify the continuous NDVI raster into two categories:

  • Low (\(NDVI\leq0.2\)) get the value of 0
  • High (\(NDVI>0.2\)) get the value of 1

Here is how we can do this with R code:

The result is shown in Figure 6.2531:

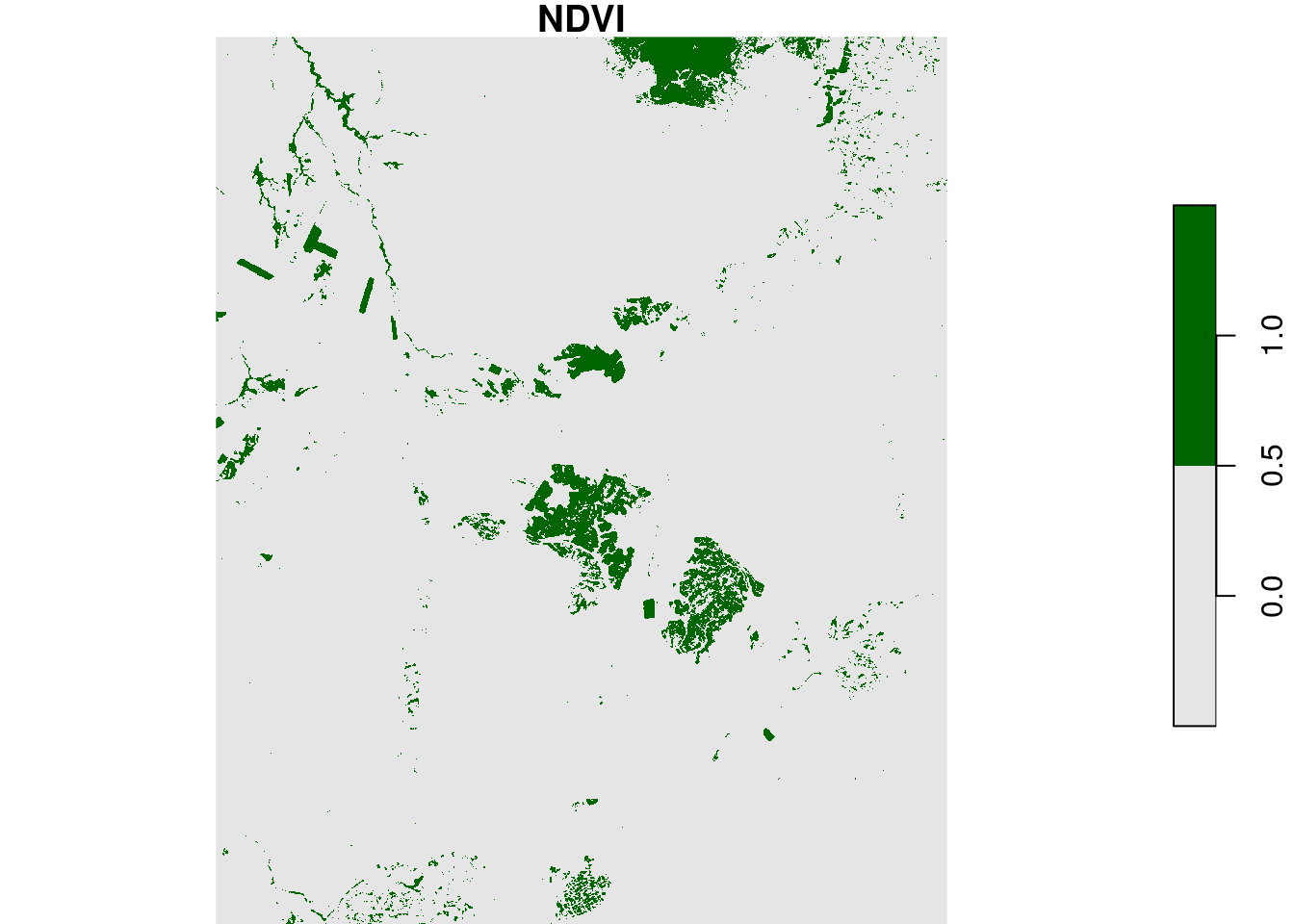
Reclassified NDVI image

Figure 6.25: Reclassified NDVI image

6.6 Generalizing raster algebra with st_apply

6.6.1 Operating on each pixel

6.6.1.1 Introduction

Suppose that we have a small raster named s, with two layers:

and that we would like to add up the two layers, plus a constant value of 10. We have already seen this is a raster algebra operation that can be achieved with arithmetic operators:

But what if we want to apply a function on three, ten, or a hundred layers? Specifying each and every layer is impractical in such case. For that, we have a more general raster algebra approach using st_apply. The st_apply function is very similar to apply (Section 4.5). It takes an object, the dimension indices we wish to operate on, and a function, then applies the function on each subset along the dimension(s).

For example, the following expression calculates the same raster u as shown above, using st_apply:

The st_apply function thus makes it possible to summarize raster dimension(s) properties using various built-in functions, such as mean, sum, min, max, etc., as well as custom functions, such as function(x) sum(x)+10.

The FUN parameter determines the function which is going to be applied on each subset of the chosen dimension, just like in apply (Section 4.5). In case the dimension we operate on is 1:2, i.e., “pixels” (Section 5.2.3), the FUN parameter determines the function which calculates each pixel value in the output raster, given the respective pixel values of the input raster from all layers.

The FUN function needs to accept a vector of any length and return either one of the following:

  • A vector of length 1, in which case st_apply returns a single-band raster, or
  • A vector of (fixed) length n, in which case st_apply returns a multi-band raster with n layers

6.6.1.2 NDVI

As another example, the above expression to calculate NDVI:

Can be replaced with the following analogous expression using st_apply:

6.6.1.3 Pixel means

As another example, the following expression uses st_apply along with FUN=mean to calculate a new raster with the average NDVI values (during the period 2000-2019) per pixel, based on the raster r. The additional na.rm=TRUE argument is passed to the function (mean, in this case). This makes the calculation ignore NA values:

The resulting average NDVI raster is shown in Figure 6.26:

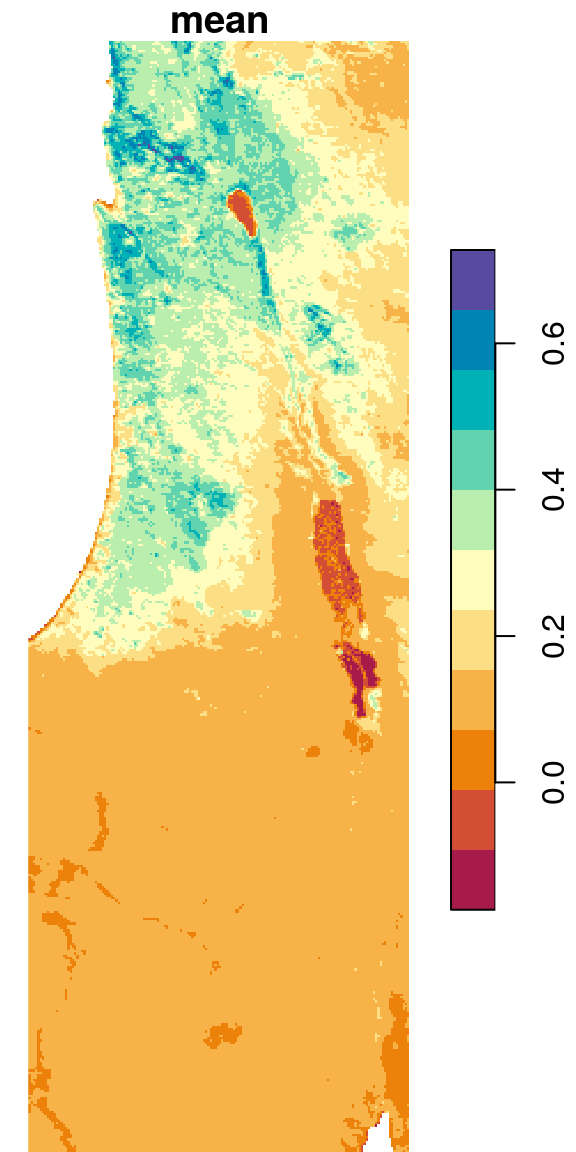
Average NDVI per pixel

Figure 6.26: Average NDVI per pixel

6.6.1.4 Pixel ranges

In the following example we use the range function, which is a function that returns a vector of length 2:

Why do we use the more complex function f which includes a conditional, rather then just using FUN=range? The function is more complex in this case, to avoid the situation when all values are NA, in which case range returns c(Inf, -Inf):

Instead, we want the function to return c(NA, NA):

Printing the resulting raster shows that the new (min-max) dimension is set as the first one, while dimensions "x" and "y" are set as 2 and 3, respectively:

The standard arrangement, where "x" and "y" dimensions are 1 and 2, respectively, while other dimensions (if any) begin at 3 is more convenient. To reorder dimensions, we can use the aperm function. The function accepts a stars object, and the new dimension order. For example, in this case we would like the the first two dimensions to be 2 and 3, followed by dimension 1:

The last operation uses indices, which means we need to know in advance that dimensions "x" and "y" are in positions 2 and 3. A more general expression, using nothing but dimension names is given below. This expression puts the "x" and "y" dimensions first, and the third dimension last, regardless of their initial order:

One more thing we may want to do is give the dimension informative names:

The result is shown in Figure 6.27:

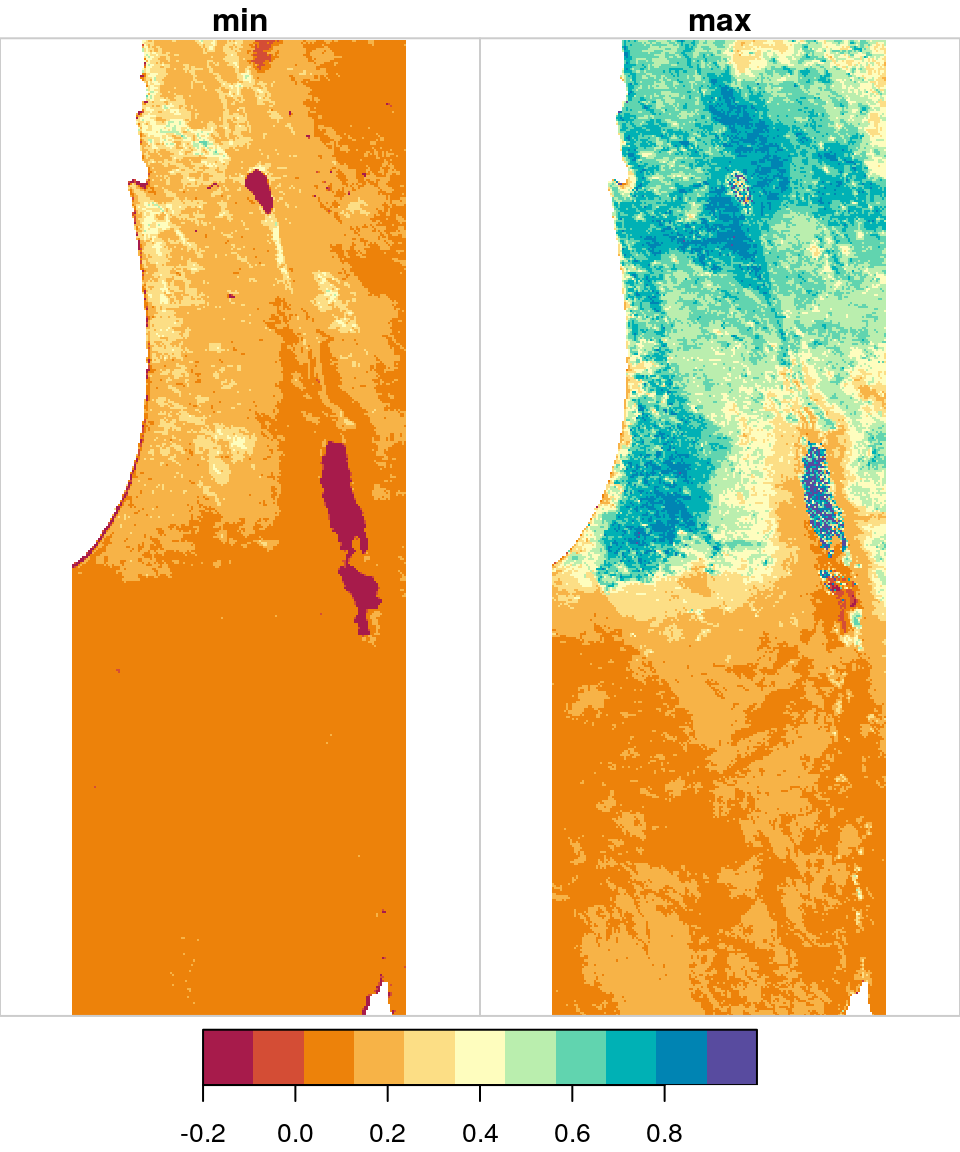
Minimum and maximum NDVI value per pixel

Figure 6.27: Minimum and maximum NDVI value per pixel

Why does the resulting raster have two layers? What is the meaning of each layer?

6.6.1.5 Pixel amplitudes

We can take the result from Section 6.6.1.4 and further calculate the difference between the maximum and minimum NDVI, i.e., the observed amplitude of NDVI values, in the raster r. The function being applied is diff, to find the difference between the minimum and maximum values per pixel:

The result is shown in Figure 6.28:

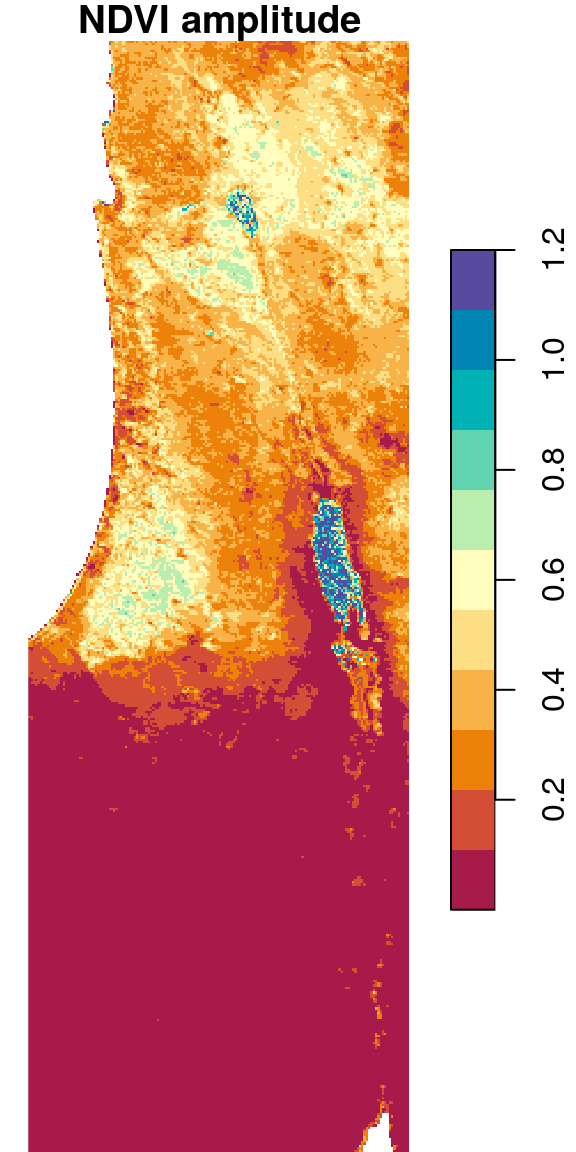
Amplitude of NDVI values per pixel

Figure 6.28: Amplitude of NDVI values per pixel

6.6.1.6 Pixel NA proportions

Another practical use case for st_apply is calculating the proportion of NA values per pixel:

The result in shown in Figure 6.29:

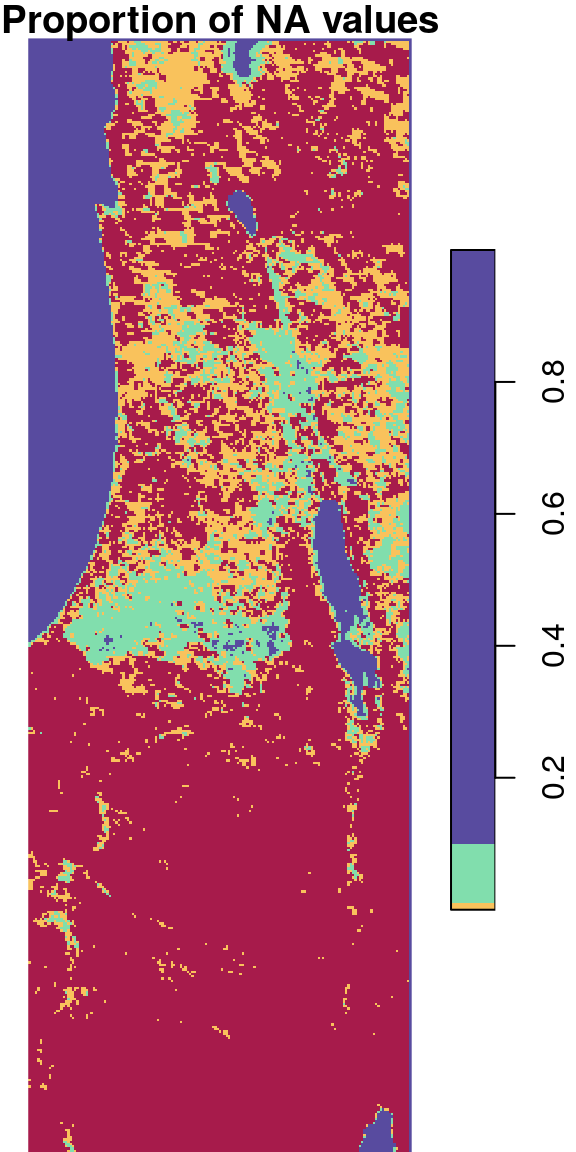
Proportion of `NA` values per pixel

Figure 6.29: Proportion of NA values per pixel

Note that we are using logarithmic breaks since the distribution of NA proportion values is very skewed:

For example, the pixels where proportion of NA values is between 0 and 0.001 is shown in red, and so on.

6.6.2 Operating on each layer

In Section 6.6.1 we have seen examples of applying a function on the value of each pixel, using MARGIN=1:2. Another useful mode of operation with st_apply is summarizing the properties of each layer, rather than each pixel. This is achieved with MARGIN=3. For example, the following expressions calculate the minimum, mean and maximum NDVI value across the entire image per layer (i.e., per month):

The resulting stars objects are one-dimensional. Accordingly, layer_mean[[1]], layer_min[[1]] and layer_max[[1]] are one-dimensional arrays. One-dimensional arrays are treated as numeric vectors in most cases. For example, the following expression returns the average NDVI values of the first 10 layers in r:

The three resulting time series can therefore be visualized as follows (Figure 6.30):

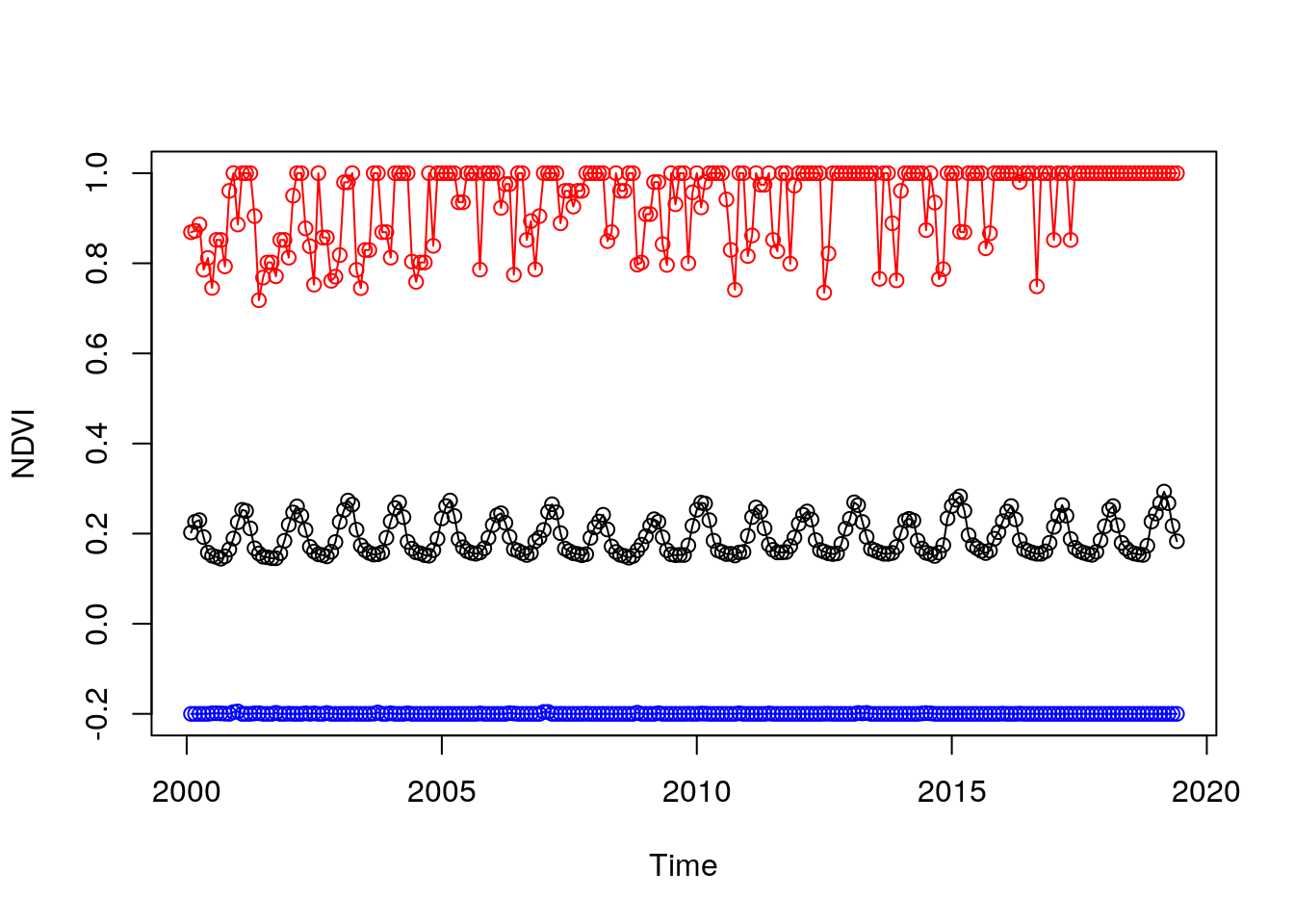
Minimum, mean and maximum NDVI over time

Figure 6.30: Minimum, mean and maximum NDVI over time

  1. http://rpubs.com/etiennebr/visualraster↩

  2. https://landsat.usgs.gov/what-are-band-designations-landsat-satellites↩

  3. https://datacarpentry.org/organization-geospatial/01-spatial-data-structures-formats/index.html↩

  4. This type of a false color image mapping emphasizes green vegetation (in red).↩

  5. http://rpubs.com/etiennebr/visualraster↩

  6. We can also do the above reclassification with a single expression, using cut(ndvi, breaks = c(-Inf, 0.2, Inf)). This becomes especially convenient if we have numerous categories or classes. The result consists of values of type factor, which we don’t go into in this book.↩