Chapter 1 The R environment

Last updated: 2020-08-12 00:35:48

Aims

Our aims in this chapter are:

Introduce the main advantages and properties of programming
Introduce the R environment
Learn to write and execute basic expressions in R

1.1 Programming

1.1.1 Why is programming necessary?

1.1.1.1 A CSV file

Is this (Figure 1.1) a Microsoft Excel spreadsheet?

Figure 1.1: CSV file

The file has an Excel icon, and it opens in Excel on double-click (Figure 1.2).

Figure 1.2: CSV file opened in Excel

However, this is in fact a plain-text file in the Comma Separated Values (CSV) format, and can be opened in various other software, such as Notepad (Figure 1.3).

Figure 1.3: CSV file opened in Notepad

The graphical interface “protects” us from the little details:

Hiding the .csv file extension
Displaying an Excel icon
Automatically opening the file in Excel

Is this a bad thing? Often, it is:

We can be unaware of the fact that the file can be opened in software other than Excel
In general—the “ordinary” interaction with the computer is limited to clicking on links, selecting from menus and filling dialog boxes
The latter approach suggests there are “boundaries” set by the computer interface for the user who wishes to accomplish a given task
Of course the opposite is true—the user has full control, and can tell the computer exactly what he wants to do

1.1.1.2 Changing a raster value

Question: how can we change the value of a particular raster cell, such as the [120, 120] cell in the rainfall.tif raster (Figure 1.4)?

Figure 1.4: The rainfall.tif raster

In ArcGIS (using the GUI), to change the value of an individual pixel we would have to go through the following steps:

Open the raster with “Add Data”
Convert the raster to points (Figure 1.5)
Calculate row and column indices
Locate the point we want to change and edit its attribute
Convert the points to back to a raster, using the same extent and resolution and setting a snap raster
Export the raster

Raster to points in ArcGIS^[https://support.esri.com/en/technical-article/000010981]

Figure 1.5: Raster to points in ArcGIS¹¹

In R, the process is much more straightforward:

Loading the stars package
Reading the rainfall.tif raster
Assigning a new value to the [120, 120] cell
Writing the raster to disk

library(stars)
r = read_stars("_book/data/rainfall.tif")
r[[1]][120, 120] = 1000
write_stars(r, "rainfall2.tif")

It is worth mentioning that an analogous workflow exists in Python:

import gdalnumeric
r = gdalnumeric.LoadFile("rainfall.tif")
r[119, 119] = 1000
gdalnumeric.SaveArray(r, "rainfall2.tif", format = "GTiff", prototype = "rainfall.tif")

1.1.2 What is programming

A computer program is a sequence of text instructions that can be “understood” by a computer and executed. A programming language is a machine-readable artificial language designed to express computations that can be performed by a computer. Programming is the preferred way for giving instructions to the computer because that way:

We break free from the limitations of the graphical interface, and are able to perform tasks that are unfeasible or even impossible
We can keep the code for editing and re-use in the future, and as a reminder to ourselves of what we did in the past
Sharing a precise record of our analysis with others, making our results reproducible

1.1.3 Computer hardware

When learning programming in R, at times we will refer to specific components of the computer hardware. Here are the main ones (Figure 1.1.3):

The Central Processing Unit (CPU) performs (simple) calculations very fast
The Random Access Memory (RAM) is a short-term fast memory
Mass Storage (e.g., hard drive) is long-term and high-capacity memory, but slow
A Keyboard is an example of an input device
A Screen is an example of an output device

Figure 1.6: Components of a computing environment

1.1.4 Abstraction and execution models

Programming languages differ in two main aspects: their level of abstraction and their execution models. Abstraction is the presentation of data and instructions which hide implementation detail. Abstraction is what lets the programmer focus on the task at hand, ignoring the small technical details (Figure 1.7).

Low-level programming languages provide little or no abstraction. The advantage is efficient memory use and therefore fast execution, but the disadvantage is that such languages are difficult to use, because of the many technical details the programmer needs to know.

High-level programming languages provide more abstraction and automatically handle various aspects, such as memory use. The advantage of high-level languages is that they are more “understandable” and easier to use. The disadvantage is that high-level languages can be less efficient and therefore slower.

Figure 1.7: Increasing abstraction from Assembly to C++ to R

Execution models are systems for execution of programs written in a given programming language. In compiled execution models, before being executed the code needs to be compiled into executable machine code. In compiled execution models, the code is first translated to an executable file (Figure 1.8). Subsequently, the executable file can then be run (Figure 1.9). In interpreted execution models, the code can be run directly, using the interpreter (Figure 1.10). The advantage of the interpretation approach is that it is easier to develop and use the language. The disadvantage, again, is lower efficiency.

Figure 1.8: Compilation of C++ code

Figure 1.9: Running an executable file

Figure 1.10: Running R code

R—along with Python, and other language—belongs in the group of high-level interpreted languages (Figure 1.11).

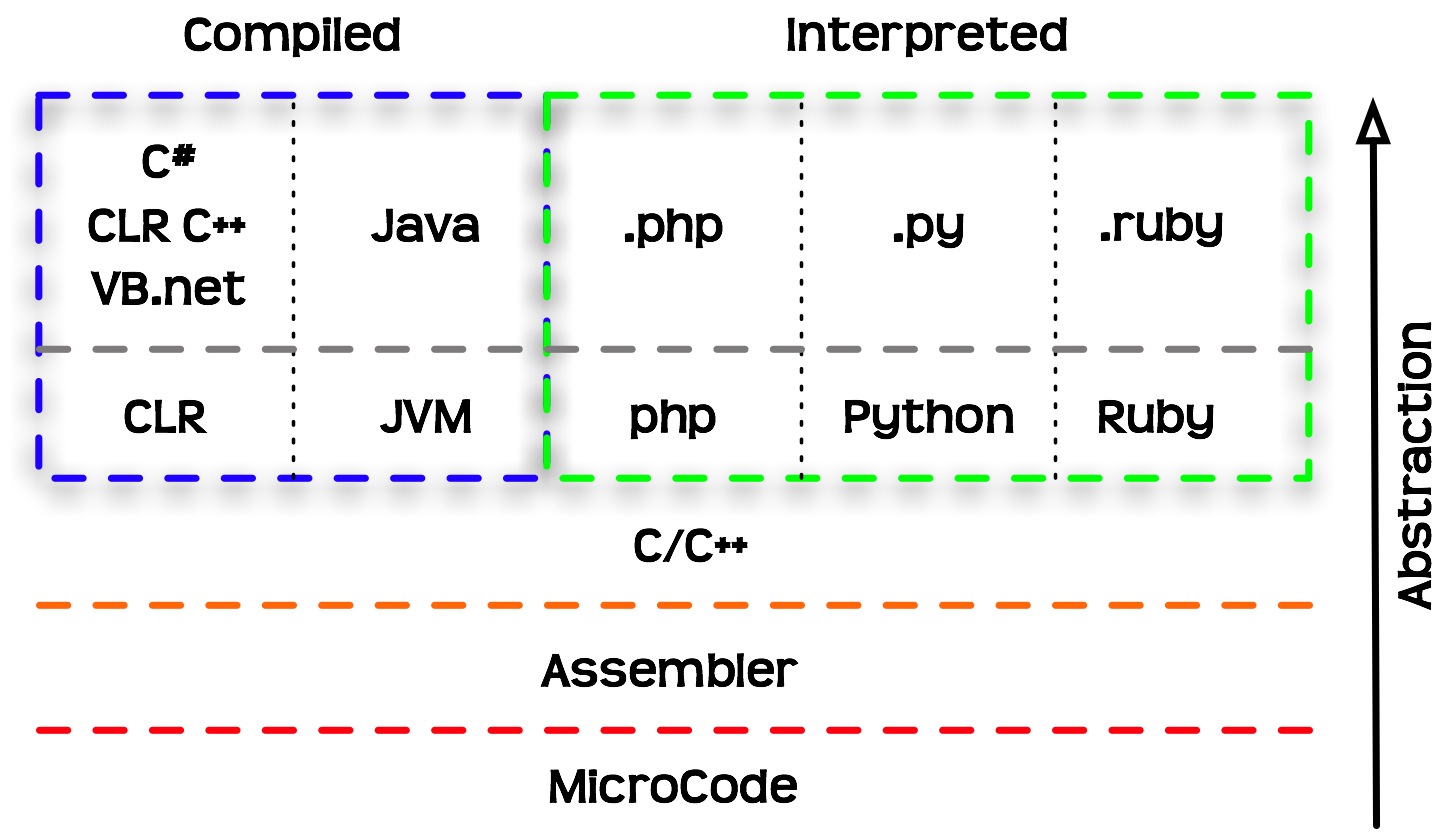
Figure 1.11: Programming languages classified based on abstraction levels and execution models

1.1.5 Object-oriented programming

In object-oriented programming, the interaction with the computer takes places through objects. Each object belongs to a class: an abstract structure with certain properties. Objects are in fact instances of a class.

The class comprises a template which sets the properties and methods each object of that class should have, while an object contains specific values for that particular instance (Figure 1.12).

For example:

All cars we see in the parking lot are instances of the “car” class
The “car” class has certain properties (manufacturer, color, year) and methods (start, drive, stop)
Each “car” object has specific values for the properties (Suzuki, brown, 2011)

An object^[https://www.w3schools.com/js/js_objects.asp]

Figure 1.12: An object¹²

In R, as we will see later on, everything we work with are objects. For example, a raster (such as rainfall.tif) that we import into R is actually translated to an object of a class named stars. The object has numerous properties, such as the number of rows an columns, the resolution, the Coordinate Reference System (CRS), and so on:

library(stars)
r = read_stars("_book/data/rainfall.tif")

r
## stars object with 2 dimensions and 1 attribute
## attribute(s):
##  rainfall.tif   
##  Min.   :200.0  
##  1st Qu.:376.9  
##  Median :502.0  
##  Mean   :484.7  
##  3rd Qu.:585.2  
##  Max.   :908.5  
##  NA's   :20717  
## dimension(s):
##   from  to  offset delta                       refsys point values    
## x    1 153  615965  1000 +proj=utm +zone=36 +ellps... FALSE   NULL [x]
## y    1 240 3691819 -1000 +proj=utm +zone=36 +ellps... FALSE   NULL [y]

1.1.6 Inheritance

One of the implications of object-oriented programming is inheritance. Inheritance makes it possible for one class to “extend” another class, by adding new properties and/or new methods. For example:

A “taxi” class is an extension of the “car” class
A “taxi” has new properties (taxi company name), and new methods (switching the taximeter on and off)

In R, the idea of inheritance is realized in various ways. For example, every complex object (such as a raster) is actually a collection of smaller components (the properties):

str(r)
## List of 1
##  $ rainfall.tif: num [1:153, 1:240] NA NA NA NA NA NA NA NA NA NA ...
##  - attr(*, "dimensions")=List of 2
##   ..$ x:List of 7
##   .. ..$ from  : num 1
##   .. ..$ to    : num 153
##   .. ..$ offset: num 615965
##   .. ..$ delta : num 1000
##   .. ..$ refsys:List of 2
##   .. .. ..$ input: chr "unknown"
##   .. .. ..$ wkt  : chr "BOUNDCRS[\n    SOURCECRS[\n        PROJCRS[\"unknown\",\n            BASEGEOGCRS[\"unknown\",\n                "| __truncated__
##   .. .. ..- attr(*, "class")= chr "crs"
##   .. ..$ point : logi FALSE
##   .. ..$ values: NULL
##   .. ..- attr(*, "class")= chr "dimension"
##   ..$ y:List of 7
##   .. ..$ from  : num 1
##   .. ..$ to    : num 240
##   .. ..$ offset: num 3691819
##   .. ..$ delta : num -1000
##   .. ..$ refsys:List of 2
##   .. .. ..$ input: chr "unknown"
##   .. .. ..$ wkt  : chr "BOUNDCRS[\n    SOURCECRS[\n        PROJCRS[\"unknown\",\n            BASEGEOGCRS[\"unknown\",\n                "| __truncated__
##   .. .. ..- attr(*, "class")= chr "crs"
##   .. ..$ point : logi FALSE
##   .. ..$ values: NULL
##   .. ..- attr(*, "class")= chr "dimension"
##   ..- attr(*, "raster")=List of 3
##   .. ..$ affine     : num [1:2] 0 0
##   .. ..$ dimensions : chr [1:2] "x" "y"
##   .. ..$ curvilinear: logi FALSE
##   .. ..- attr(*, "class")= chr "stars_raster"
##   ..- attr(*, "class")= chr "dimensions"
##  - attr(*, "class")= chr "stars"

The benefit of inheritance is that the programmer does not need to write every class from scratch. Instead, new classes can be built on top of existing ones, while re-using their properties and methods.

1.2 Starting R

To use R we first need to install it. R can be downloaded from the R-project website. The current version is 3.6.1. Once R is installed, we can open the default interface (RGui) with Start → All Programs → R → R x64 3.6.1 (Figure 1.13).

Figure 1.13: RGui

We will be working with R through a more advanced interface than the default one, called the RStudio. It can be downloaded from the RStudio company website. The current version is 1.2.5001. Once both R and RStudio are installed, we can open RStudio with Start → All Programs → RStudio → RStudio (Figure 1.14).

Figure 1.14: RStudio

In this Chapter, we will only work with the console (Figure 1.15), i.e., the command line. In the following lessons we will also work with other RStudio panels.

Figure 1.15: RStudio console

1.3 Basic R expressions

1.3.1 Console input and output

We can type expressions in the console and press Enter. For example, let’s type the expression 1+3+5+7:

1 + 3 + 5 + 7
## [1] 16

The expression 1+3+5+7 was sent to the processor, and the result 16 was printed in the console. (Later on we will discuss the [1] part). Note that the value 16 is not kept in in the RAM or Mass Storage, just printed on screen (Figure 1.16).

Figure 1.16: Execution of a simple expression in R

The input and output appear like this in the slides:

1 + 3 + 5 + 7
## [1] 16

The way it input and output appear in RStudio is shown in Figure 1.17.

Figure 1.17: RStudio console input and output

We can type a number, the number itself is returned:

600
## [1] 600

We can type text inside single ' or double " quotes:

"Hello"
## [1] "Hello"

Both of these are constant values, numeric or character, the simplest type of expressions in R.

1.3.2 Arithmetic operators

Through interactive use of the command line we can experiment with basic operators in R. For example, R includes the standard arithmetic operators (Table 1.1).

Table 1.1: Arithmetic operators
Operator	Meaning
`+`	Addition
`-`	Subtraction
`*`	Multiplication
`/`	Division
`^`	Exponent

For example:

5 + 3
## [1] 8

4 - 5
## [1] -1

1 * 10
## [1] 10

1 / 10
## [1] 0.1

10 ^ 2
## [1] 100

We can use the up ↑ and down ↓ keys to scroll through the executed expressions history.

Very large or very small numbers are formatted in exponential notation:

1 / 1000000 # 1*10^-6
## [1] 1e-06

7 * 100000  # 7*10^5
## [1] 7e+05

Infinity is treated as a special numeric value Inf or -Inf:

1 / 0
## [1] Inf

-1 / 0
## [1] -Inf

Inf + 1
## [1] Inf

-1 * Inf
## [1] -Inf

We can control operator precedence with brackets, just like in math. This is recommended for clarity even where not strictly required:

2 * 3 + 1
## [1] 7

2 * (3 + 1)
## [1] 8

1.3.3 Spaces and comments

The interpreter ignores everything to the right of the number symbol #:

1 * 2 # * 3
## [1] 2

The # symbol is therefore used for code comments:

# Multiplication example
5 * 5
## [1] 25

Why do you think the code outputs are marked by ## in the code sections (such as ## [1] 25 in the above code section)?

The interpreter ignores spaces, so the following expressions are treated exactly the same way:

1 + 1
## [1] 2

1+1
## [1] 2

1+           1
## [1] 2

We can type Enter in the middle of an expression and keep typing on the next line. The interpreter displays the + symbol, which means that the expression is incomplete (Figure 1.18):

5 * 
2
## [1] 10

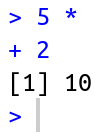
Figure 1.18: Incomplete expression

We can also:

Exit from the “completion” state, or from an ongoing computation, by pressing Esc
Clear the console with Ctrl+L

1.3.4 Conditional operators

Conditions are expressions that use conditional operators and have a yes/no result, i.e., the condition can be either true or false. The result of a condition is a logical value, TRUE or FALSE:

TRUE means the expression is true
FALSE means the expression is false
(NA means it is unknown)

The conditional operators in R are listed in Table 1.2.

Table 1.2: Conditional operators
Operator	Meaning
`==`	Equal
`>`	Greater than
`>=`	Greater than or equal
`<`	Less than
`<=`	Less than or equal
`!=`	Not equal
`&`	And
`\|`	Or
`!`	Not

For example, we can use conditional operators to compare numeric values:

1 < 2
## [1] TRUE

1 > 2
## [1] FALSE

2 > 2
## [1] FALSE

2 >= 2
## [1] TRUE

2 != 2
## [1] FALSE

“Equal” (==) and “not equal” (!=) are opposites of each other, since a pair of values can be either equal or not:

1 == 1
## [1] TRUE
1 != 1
## [1] FALSE

1 == 2
## [1] FALSE
1 != 2
## [1] TRUE

The “and” (&) and “or” (|) operators are used to create more complex conditions. “And” (&) returns TRUE when both sides are TRUE:

(1 < 10) & (10 < 100)
## [1] TRUE

(1 < 10) & (10 > 100)
## [1] FALSE

“Or” (|) returns TRUE when at least one of the sides is TRUE:

(1 < 10) | (10 < 100)
## [1] TRUE

(1 < 10) | (10 > 100)
## [1] TRUE

The last conditional operator is “not” (!), which reverses TRUE to FALSE and FALSE to TRUE:

1 == 1
## [1] TRUE
!(1 == 1)
## [1] FALSE

(1 == 1) & (2 == 2)
## [1] TRUE
(1 == 1) & !(2 == 2)
## [1] FALSE

Run the following expression and explain their result:

FALSE == FALSE

!(TRUE == TRUE)

!(!(1 == 1))

1.3.5 Special values

R has several special values, as listed in Table 1.3.

Table 1.3: Special values in R
Value	Meaning
`Inf`	Infinity
`NA`	Not Available
`NaN`	Not a Number
`NULL`	Empty object

We already met Inf, and have shown how it can be the result of particular arithmetic operations (Section 1.3.2):

1 / 0
## [1] Inf

NA specifies an unknown, or missing, value. Later on we will see several situations where NA values can arise. For example, empty cells in a table imported into R, such as from a CSV file, is encoded in R as an NA value.

NA values can also participate in any arithmetic or logical operation. For example:

NA + 3
## [1] NA

Why do you think the result of the above expression is NA?

NaN is less relevant for the material of this book, but it is important to be familiar with it. NaN values often result from “meaningless” arithmetic operations:

0 / 0
## [1] NaN

In practice, NaN often behave the same way as NA.

Finally, the value of NULL specifies an empty object:

NULL
## NULL

NULL has some uses which we will discuss later on (e.g., Section 4.2.3).

1.3.6 Functions

In math, a function (Figure 1.19) is a relation that associates each element x of a set X, to a single element y of another set Y. For example, the function \(y=2x\) is a mathematical function that associates any number \(x\) with the number \(2x\).

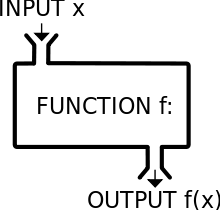
Figure 1.19: A function

The concept of functions in programming is similar. A function is a code piece that “knows” how to do a certain task. Executing the function is known as a function call. The function accepts zero or more objects as input (e.g., 2) and returns a single object as output (e.g., 4), possibly also doing other things known as side effects.

The number and type of inputs the function needs are determined in the function definition; these are known as the function parameters (e.g., a single number). The objects the function received in practice, as part of a particular function call, are known as arguments (e.g., 2).

A function is basically a set of pre-defined instructions. There are thousands of built-in functions in R. Later on we will learn to define our own functions (Section 3.3).

A function call is composed of the function name, followed by the arguments inside brackets () and separated by commas ,:

sqrt(4)
## [1] 2

The sqrt (square root) function received a single argument 4 and returned its square root 2.

In fact, everything we do in R involves functions (Figure 1.20).

Figure 1.20: From Chambers 2014, Statistical Science (https://arxiv.org/pdf/1409.3531.pdf)

Even arithmetic operators are functions that are written in a special way. They can also be written in the ordinary syntax of functions, as follows:

`+`(5, 5)
## [1] 10

1.3.7 Error messages

Consider the following expressions:

sqrt(16)
## [1] 4

sqrt("a")
## Error in sqrt("a"): non-numeric argument to mathematical function

sqrt(a)
## Error in eval(expr, envir, enclos): object 'a' not found

In last two expressions we got error messages, because the expressions were illegal, i.e., not in agreement with the syntax rules of R. The first error occurred because we tried to run a mathematical operation sqrt on a text value "a". The second error occurred because we tried to use a non-existing object a. And text without quotes is treated as a name of an object, i.e., a label for an actual object stored in RAM. Since we don’t have an object named a we got an error.

1.3.8 Pre-loaded objects

When starting R, a default set of objects is loaded into the RAM, such as TRUE, FALSE, sqrt and pi. For example, type pi and see what happens:

pi
## [1] 3.141593

1.3.9 Decimal places

Is the value of PI stored in memory really equal to 3.141593?

pi == 3.141593
## [1] FALSE

If not, what is the difference?

pi - 3.141593
## [1] -3.464102e-07

The reason is that by default R prints only the first 7 digits:

options()$digits
## [1] 7

1.3.10 Case-sensitivity

R is case-sensitive, it distinguishes between lower-case and upper-case letters. For example, TRUE is a logical value, but True and true are undefined:

TRUE
## [1] TRUE

True
## Error in eval(expr, envir, enclos): object 'True' not found

true
## Error in eval(expr, envir, enclos): object 'true' not found

1.3.11 Classes

R is an object-oriented language (Section 1.1.5), where each object belongs to a class. The class functions accepts an object and returns the class name:

class(TRUE)
## [1] "logical"

class(1)
## [1] "numeric"

class(pi)
## [1] "numeric"

class("a")
## [1] "character"

class(sqrt)
## [1] "function"

Explain the returned value of the following expressions.

class(1 < 2)
## [1] "logical"

class("logical")
## [1] "character"

class(1) == class(2)
## [1] TRUE

class(class)
## [1] "function"

class(class(sqrt))
## [1] "character"

class(class(1))
## [1] "character"

1.3.12 Using help files

Every built-in object is associated with a help document, which can be accessed using the help function or the ? operator:

help(class)
?class
?TRUE
?pi