E Exercise 03

Last updated: 2024-07-28 11:47:09

E.1 Materials

The materials for this exercise are:

  • Matrices and rasters (Chapter 5)
  • Raster processing (Chapter 6)

E.2 Question 1

  • Read the raster MOD13A3_2000_2019.tif to a multi-band raster object named r.
  • Calculate a vector of length 24 with the correlation coefficients between the values of the layer 1, and the values of layers 1, 2, …, 24.
  • To calculate correlation coefficients use the cor function with the use='pairwise.complete.obs' argument, as in: cor(x, y, use='pairwise.complete.obs').
  • For example, the 2nd value in the vector should be equal to:
## [1] 0.9752619
  • Plot the values of the vector, as shown in Figure E.1.
  • Note: the two arguments passed to the cor function, i.e., the pixel values of layer 1 and layer n, need to be either vectors or arrays (not matrices). If necessary, a matrix can be converted to a vector with as.vector.
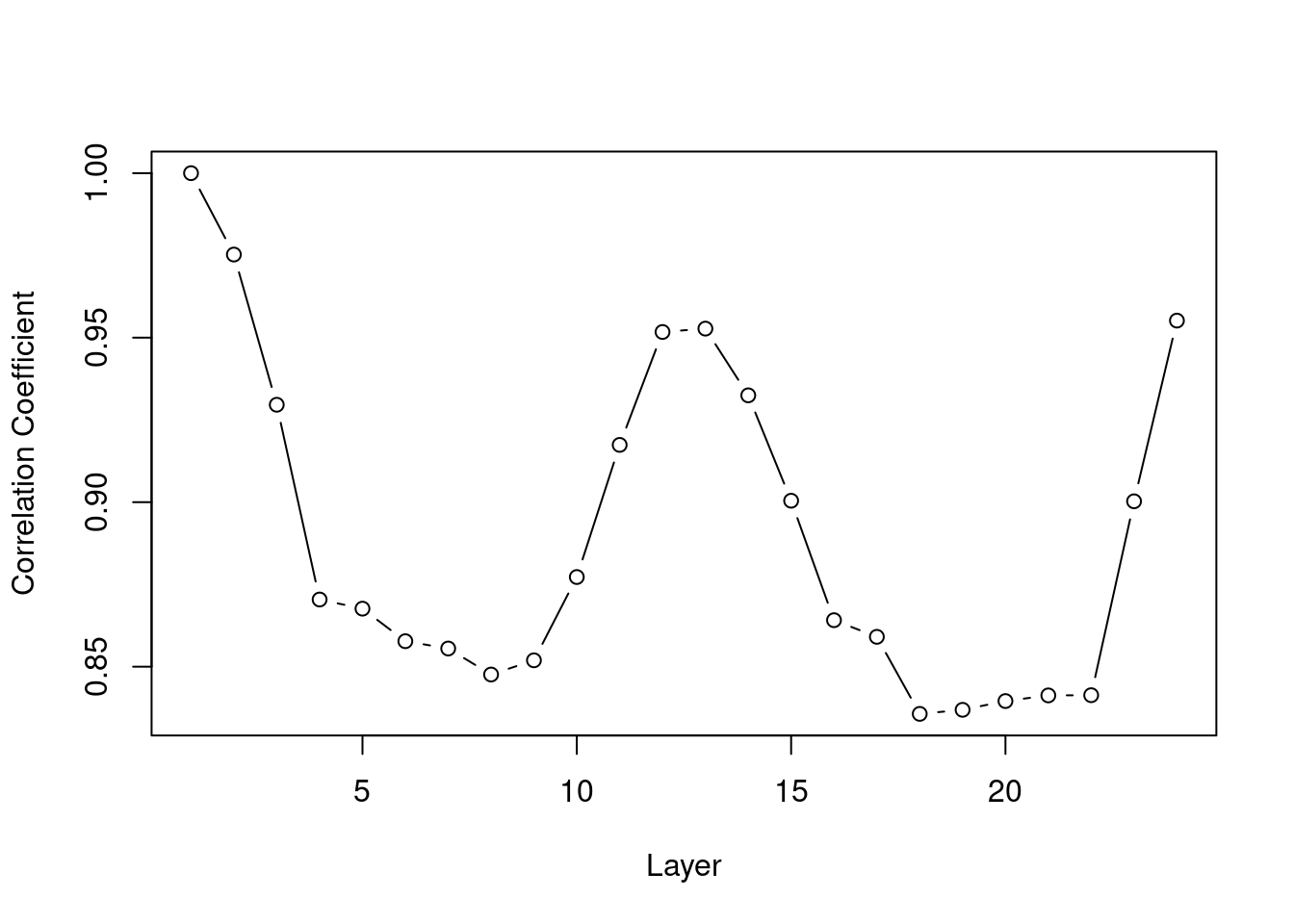
Correlation between NDVI values in layer 1 and layers 1-24

Figure E.1: Correlation between NDVI values in layer 1 and layers 1-24

(50 points)

E.3 Question 2

  • Read the raster MOD13A3_2000_2019.tif to a multi-band raster object named r.
  • Create a single-band raster s, marking areas with relatively high NDVI, relatively low NDVI, and large amount of NA, as follows:
    • Pixels where the maximal non-NA NDVI value across all 233 bands of r is <0.6, will have a value of 0 in s
    • Pixels where the maximal non-NA NDVI value across all 233 bands of r is ≥0.6, will have a value of 1 in s
    • Pixels where the proportion of NA values is >0.2 (regardless of NDVI values), will have a value of NA in s
  • Plot the raster s with values of 0 marked in 'orange' and values of 1 marked in 'darkgreen' (values of NA will be transparent, by default)
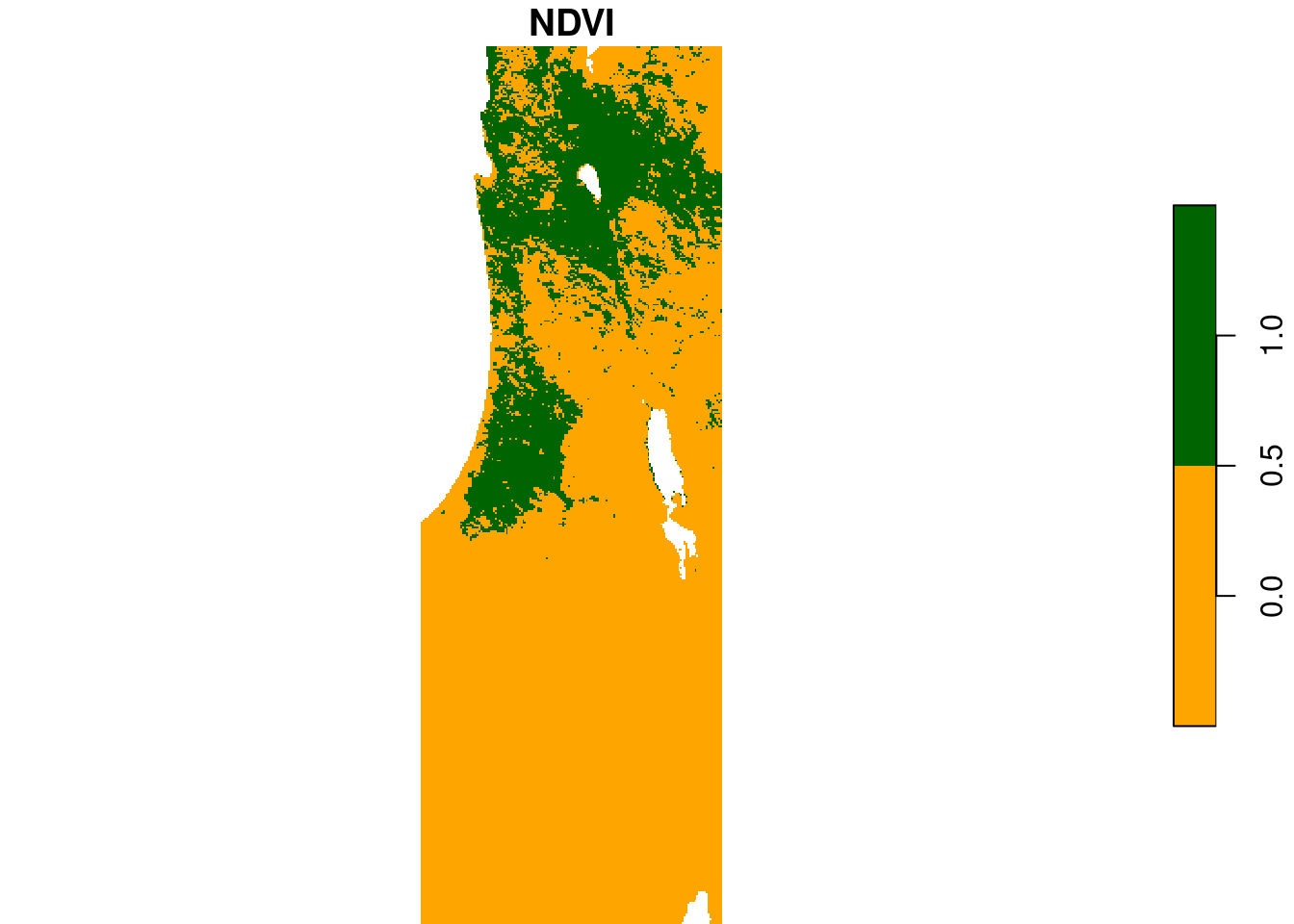
$NDVI_{max}≥0.6$ (green) and $NDVI_{max}<0.6$ (orange)

Figure E.2: \(NDVI_{max}≥0.6\) (green) and \(NDVI_{max}<0.6\) (orange)

(50 points)