Chapter 7 Vector layers

Last updated: 2024-07-28 11:42:02

Aims

Our aims in this chapter are:

• Become familiar with data structures for vector layers: points, lines and polygons
• Examine spatial and non-spatial properties of vector layers
• Create subsets of vector layers based on their attributes
• Learn to transform a layer from one Coordinate Reference System (CRS) to another

We will use the following R packages:

• sf
• mapview
• stars

7.1 Vector layers

7.1.1 What is a vector layer?

Vector layers are essentially sets of geometries associated with non-spatial attributes (Figure 7.1). The geometries are sequences of one or more point coordinates, possibly connected to form lines or polygons. The non-spatial attributes come in the form of a table.

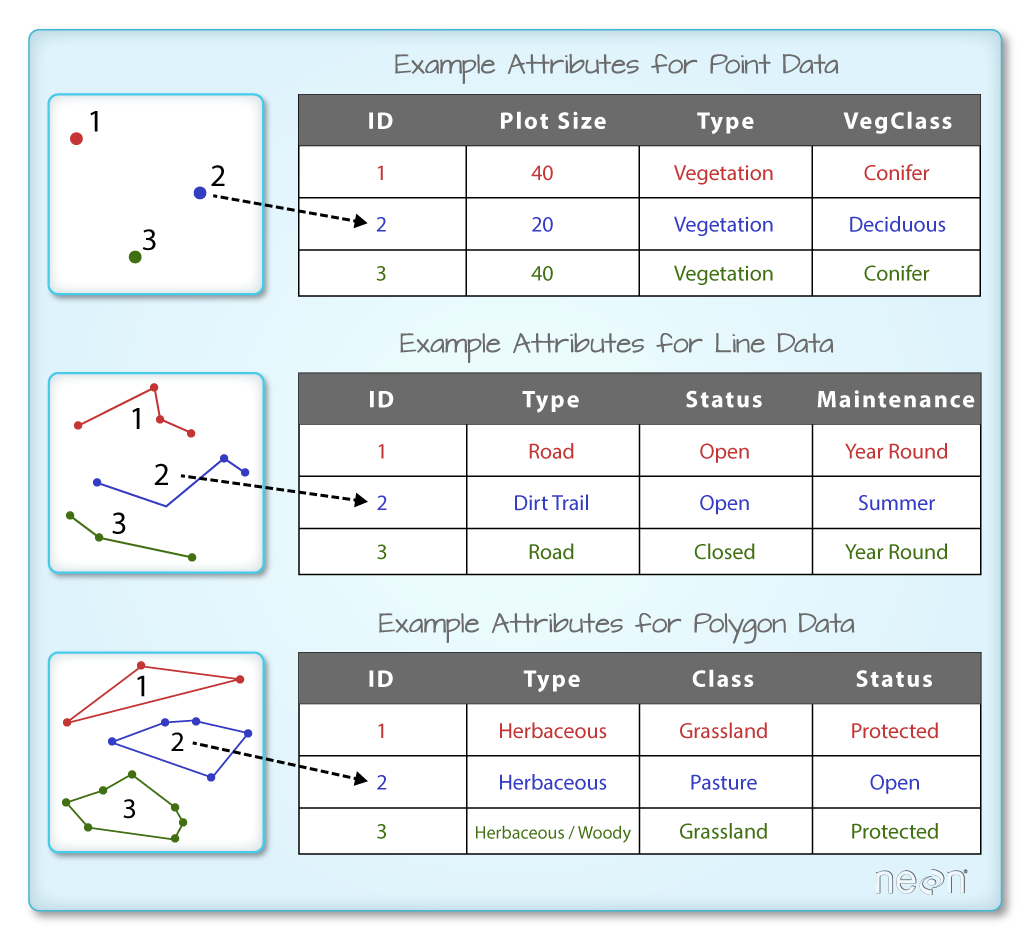
Figure 7.1: Geometry (left) and non-spatial attributes (right) of vector layers (https://www.neonscience.org/dc-shapefile-attributes-r)

7.1.2 Vector file formats

Commonly used vector layer file formats (Table 7.1) include binary formats (such as the Shapefile) and plain text formats (such as GeoJSON). Vector layers are also frequently kept in a spatial database, such as PostgreSQL/PostGIS.

Table 7.1: Common vector layer file formats

Type	Format	File extension
Binary	ESRI Shapefile	.shp, .shx, .dbf, .prj, …
	GeoPackage (GPKG)	.gpkg
Plain Text	GeoJSON	.json or .geojson
	GPS Exchange Format (GPX)	.gpx
	Keyhole Markup Language (KML)	.kml
Spatial Databases	PostgreSQL / PostGIS

7.1.3 The sp package

The first R package to establish a uniform vector layer class system was sp (2005-). Together with rgdal (2003-2023) and rgeos (2011-2023), the sp package dominated the landscape of spatial analysis in R for many years. In 2023, the rgdal and rgeos packages were removed from CRAN. The sp package is kept to support the packages depending on it, however it internally uses sf, instead of rgdal and rgeos.

The sp package defines 6 main classes for vector layers (Table 7.2):

• One for each geometry type (points, lines, polygons)
• One for geometry only and one for geometry with attributes

Table 7.2: Spatial data structures in package sp

Class	Geometry type	Attributes
SpatialPoints	Points	-
SpatialPointsDataFrame	Points	data.frame
SpatialLines	Lines	-
SpatialLinesDataFrame	Lines	data.frame
SpatialPolygons	Polygons	-
SpatialPolygonsDataFrame	Polygons	data.frame

We are not going to use sp, rgdal, or rgeos in this book, instead focusing on the newer sf package (Section 7.1.4). Nevertheless, if you are going to work with spatial data in R, it is still likely you will encounter the sp, rgdal, and rgeos packages being mentioned in forums, books, or as dependencies of other R packages, so it is important to be aware of them.

7.1.4 The sf package

The sf package (Figure 7.2), is a newer (2016-) package for working with vector layers in R, which we are going to use in this book. In recent years, sf has become the standard package for working with vector data in R, practically replacing sp, rgdal, and rgeos.

Figure 7.2: Pebesma, 2018, The R Journal (https://journal.r-project.org/archive/2018-1/)

One of the important innovations in sf is a complete implementation of the Simple Features standard. Since 2003, the Simple Features standard has been widely implemented in spatial databases (such as PostGIS), commercial GIS (e.g., ESRI ArcGIS) and forms the vector data basis for libraries such as GDAL. The Simple Features standard defines several types of geometries, of which seven are most commonly used in the world of GIS and spatial data analysis (Figure 7.6). Well Known Text (WKT), along with its binary version Well Known Binary (WKB), is a plain text format for specifying geometries which is also part of the Simple Feature specification.

The sf package depends on several external software components (installed along with the R package²⁸), most importantly GDAL, GEOS, and PROJ (Figure 7.3). These well-tested and popular open-source components are common to numerous open-source and commercial software for spatial analysis, such as QGIS and PostGIS.

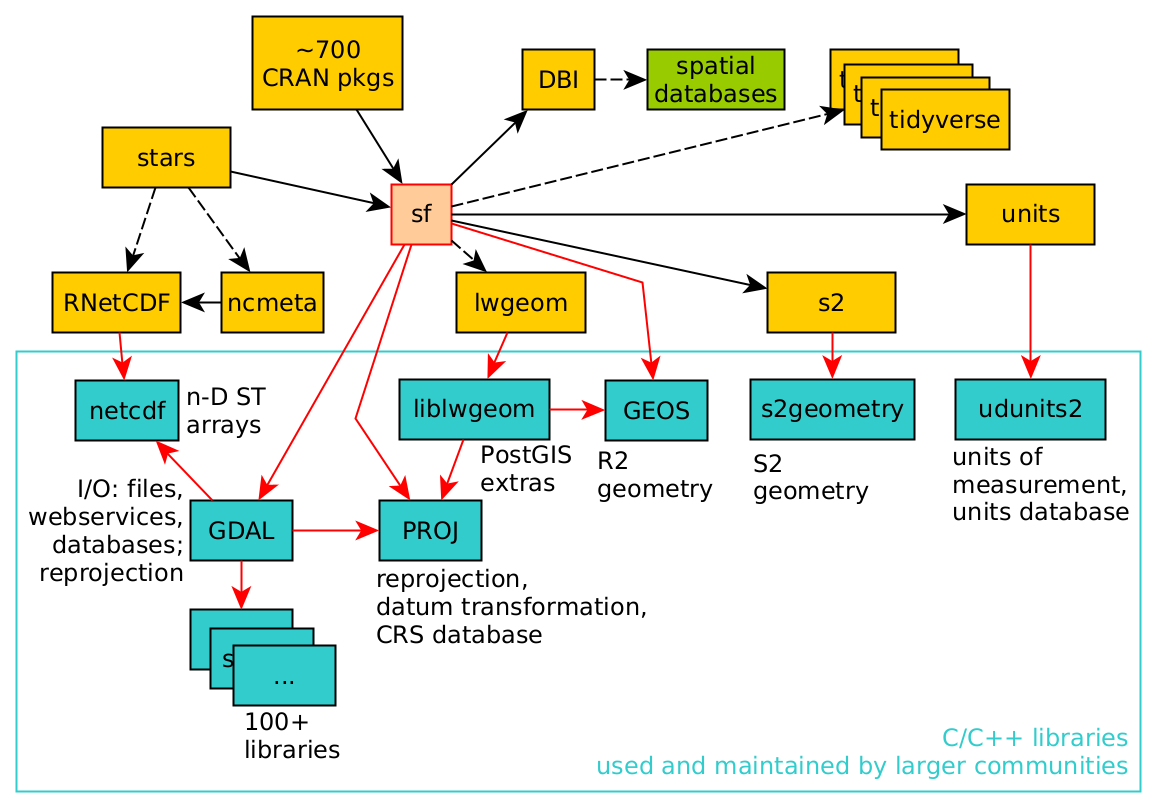
Figure 7.3: sf package dependencies (source: https://r-spatial.org/book/01-hello.html#fig-gdal-fig-nodetails)

The sf package defines a hierarchical class system, with three classes (Table 7.3):

• Class sfg—a single geometry
• Class sfc—a geometry column, which is a set of sfg geometries + CRS information
• Class sf—a layer, which is an sfc geometry column inside a data.frame with non-spatial attributes

Table 7.3: Spatial data structures in package sf

Class	Hierarchy	Information
sfg	Geometry	type, coordinates
sfc	Geometry column	set of sfg + CRS
sf	Layer	sfc + attributes

The sf class represents a vector layer by extending the data.frame class, supplementing it with a geometry column. This is similar to the way that spatial databases are structured. For example, the sample dataset shown in Figure 7.4 represents a polygonal layer with three features and six non-spatial attributes. The attributes refer to demographic and epidemiological attributes of US counties, such as the number of births in 1974 (BIR74), the number of sudden infant death cases in 1974 (SID74), and so on. The seventh column is the geometry column, containing the polygon geometries.

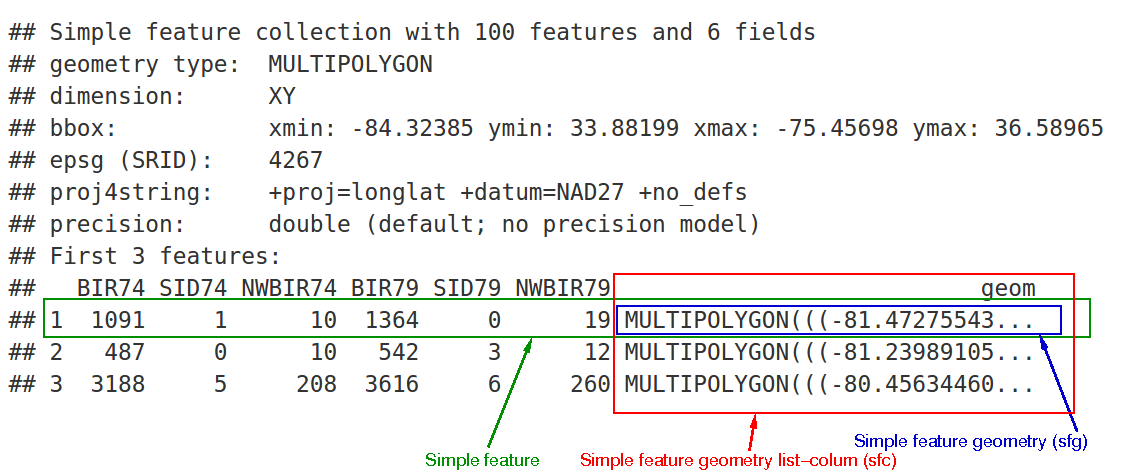
Figure 7.4: Structure of an sf object (https://cran.r-project.org/web/packages/sf/vignettes/sf1.html)

Figure 7.5 shows what the layer in Figure 7.4 would look like when mapped. We can see the outline of the three polygons, as well as the values of all six non-spatial attributes (in separate panels).

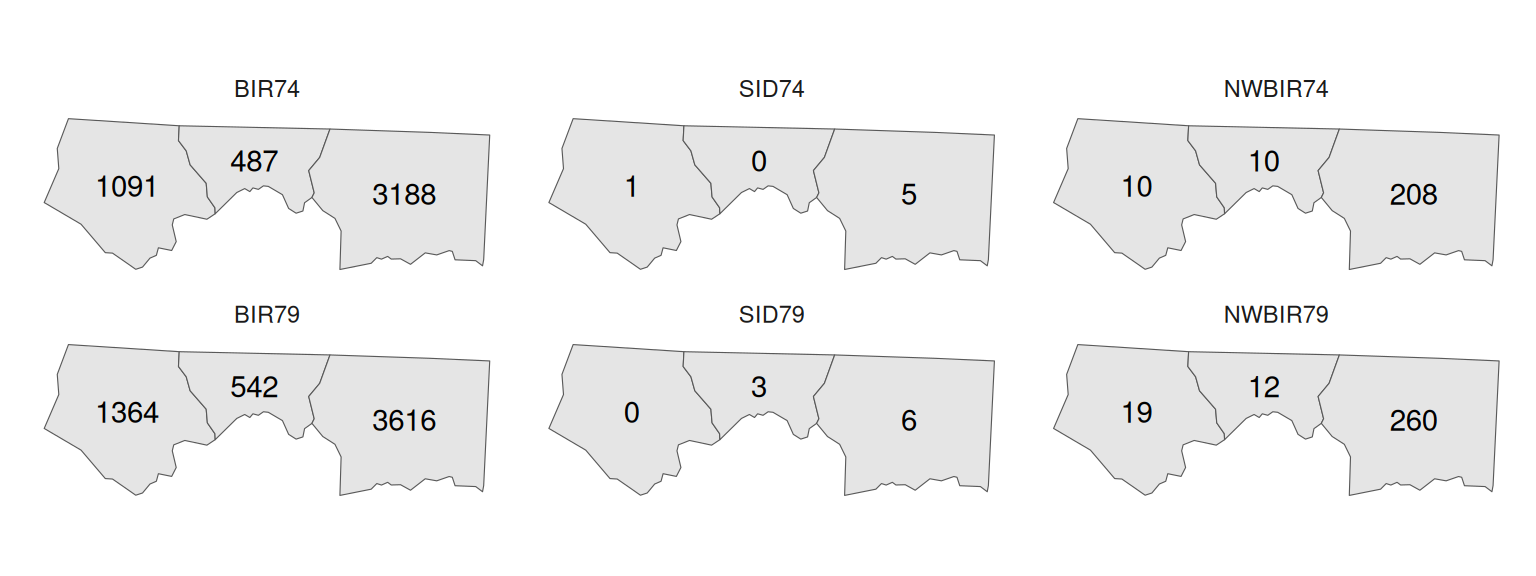
Figure 7.5: Visualization of the sf object shown in Figure 7.4

7.2 Vector layers from scratch

7.2.1 Overview

As mentioned above (Table 7.3), the sf package defines a hierarchical system of data structures, composed of three classes, from simple to complex: sfg, sfc, and sf. In this section, we are going to create an object of each of those thress classes, to learn more about them, in Sections 7.2.2, 7.2.3, and 7.2.4, respectively.

7.2.2 Geometry (sfg)

Objects of class sfg, i.e., a single geometry, can be created using the appropriate function for each geometry type:

• st_point
• st_multipoint
• st_linestring
• st_multilinestring
• st_polygon
• st_multipolygon
• st_geometrycollection

from coordinates passed as:

• numeric vectors—POINT
• matrix objects—MULTIPOINT or LINESTRING
• list objects—All other geometries

The seven most commonly used Simple Feature geometry types are displayed in Figure 7.6.

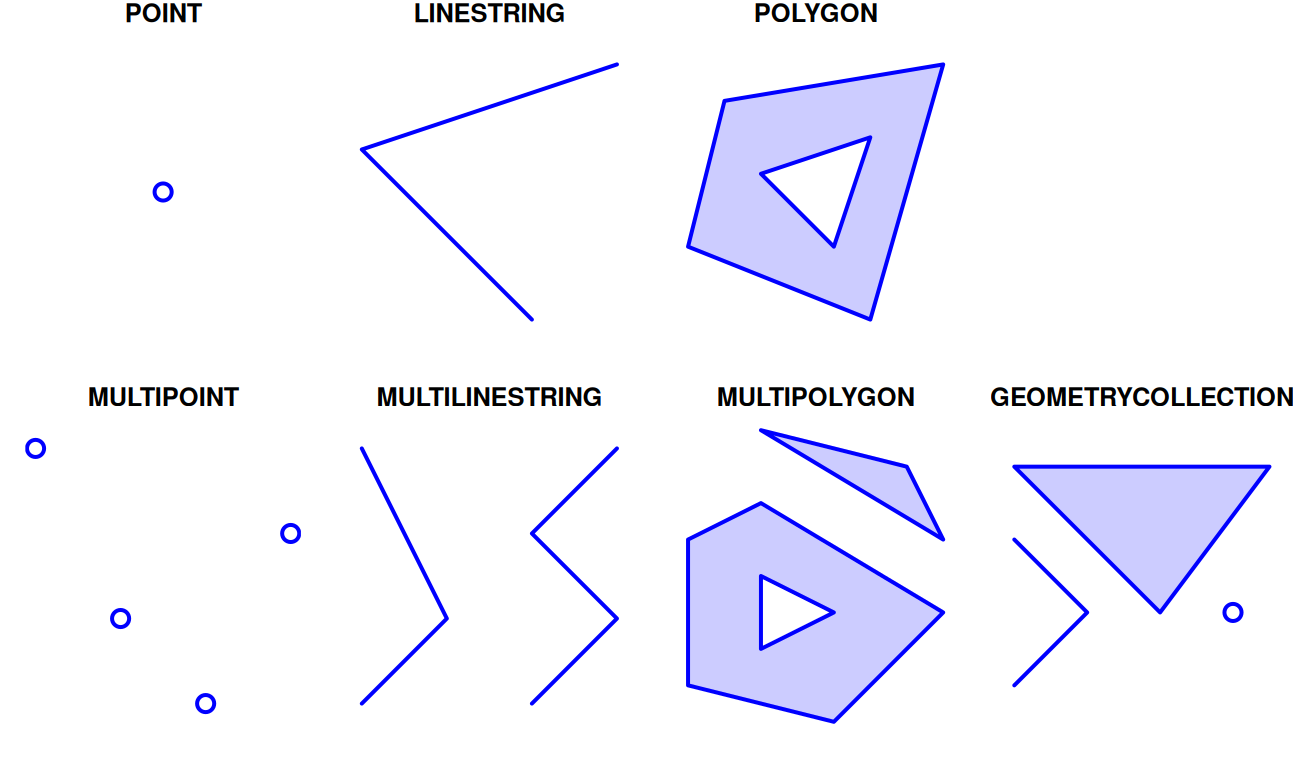
Figure 7.6: Simple feature geometry (sfg) types in package sf

Of those seven types, the GEOMETRYCOLLECTION is more rarely used and more difficult to work with. For example, the Shapefile format does not support geometries of type GEOMETRYCOLLECTION. You may wonder why does it even exist. One of the reasons is that some spatial operations may produce a mixture of geometry types. For example, the intersection (Section 8.3.4.6) between two polygons may be composed of points, lines, and polygons (Figure 7.7).

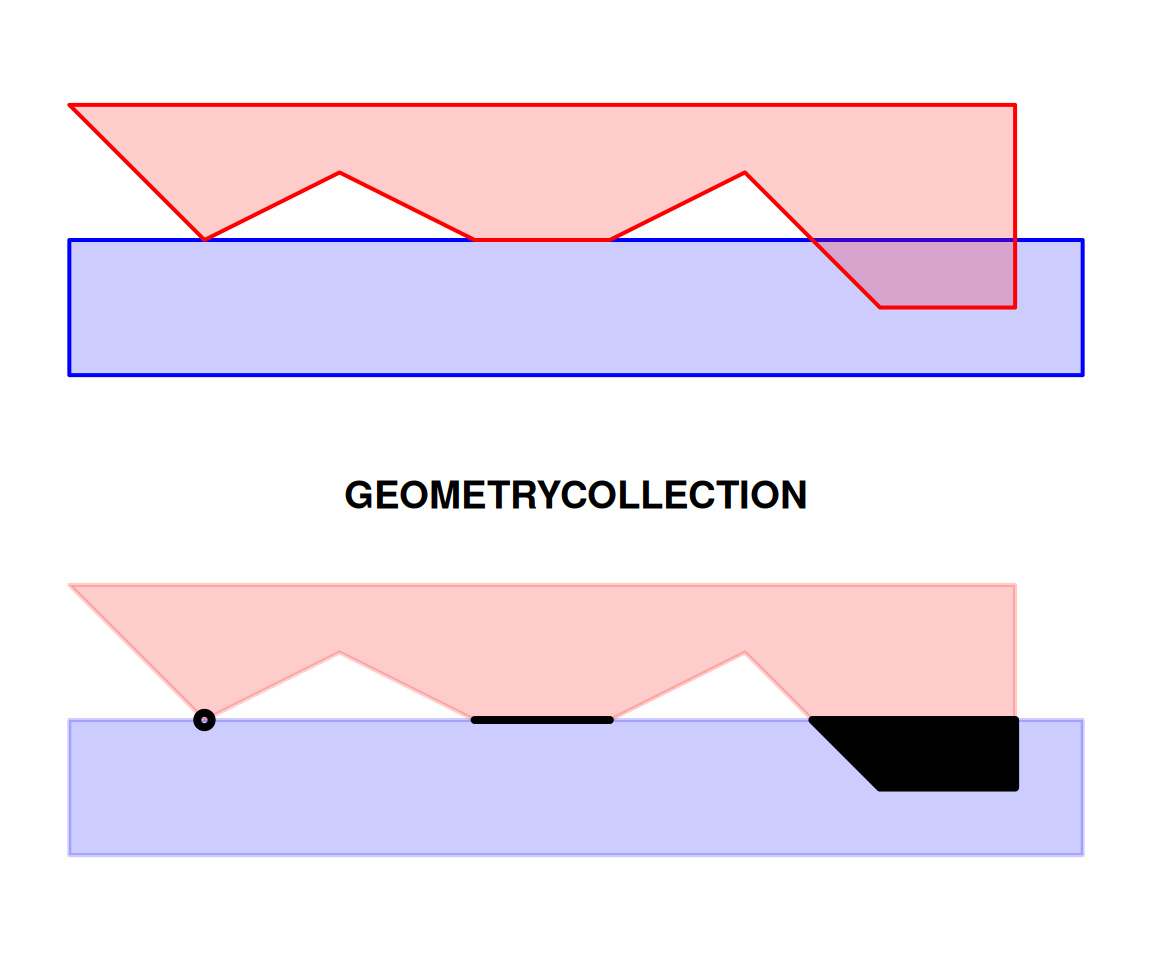
Figure 7.7: Intersection between two polygons may yield a GEOMETRYCOLLECTION

Let’s create some sfg geometries to see them in action. For example, we can create an object named pnt1, representing a POINT geometry, using the st_point function as follows:

library(sf)
pnt1 = st_point(c(34.798443, 31.243288))

Printing an sfg object in the console gives its WKT representation:

pnt1
## POINT (34.79844 31.24329)

Note that the class definition of an sfg (geometry) object is actually composed of three parts:

class(pnt1)
## [1] "XY"    "POINT" "sfg"

The meaning of each component is as follows:

• "XY"—The dimensions type (one of: "XY", "XYZ", "XYM" or "XYZM"). In this book, as in most cases of spatial analysis in general, we will be working only with two-dimensional "XY" geometries.
• "POINT"—The geometry type (one of the geometry types: "POINT", "MULTIPOINT", etc.)
• "sfg"—The general class (sfg = Simple Feature Geometry)

Here is another example of creating an sfg object. This time, we are creating a POLYGON geometry named a, using function st_polygon. (Don’t worry if the expression is unclear: we learn about using list in Chapter 11).

a = st_polygon(list(cbind(c(0,0,7.5,7.5,0),c(0,-1,-1,0,0))))

Again, printing the object shows its WKT representation:

a
## POLYGON ((0 0, 0 -1, 7.5 -1, 7.5 0, 0 0))

while class reports the dimensionality, geometry type, and general class, in that order:

class(a)
## [1] "XY"      "POLYGON" "sfg"

The polygon is displayed in Figure 7.8:

plot(a, border = 'blue', col = '#0000FF33', lwd = 2)

Figure 7.8: An sfg object of type POLYGON

Let’s create another POLYGON, named b:

b = st_polygon(list(cbind(c(0,1,2,3,4,5,6,7,7,0),c(1,0,0.5,0,0,0.5,-0.5,-0.5,1,1))))

b
## POLYGON ((0 1, 1 0, 2 0.5, 3 0, 4 0, 5 0.5, 6 -0.5, 7 -0.5, 7 1, 0 1))

class(b)
## [1] "XY"      "POLYGON" "sfg"

The second polygon is shown in Figure 7.9.

plot(b, border = 'red', col = '#FF000033', lwd = 2)

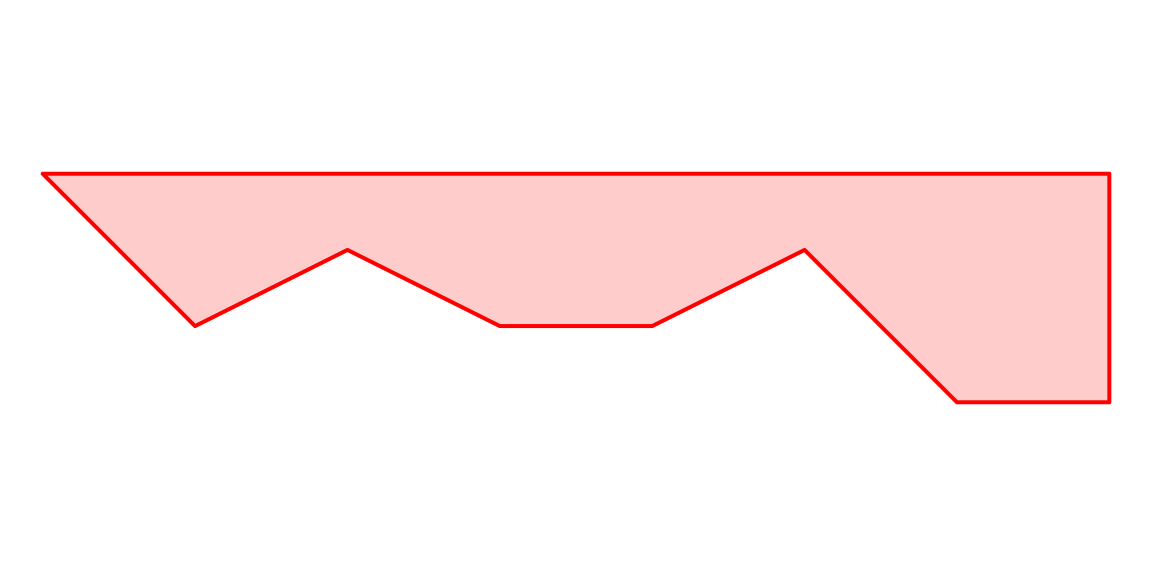
Figure 7.9: Another sfg object of type POLYGON

The c function, when given sfg geometries, combines those geometries into one. For example, combining two POLYGON geometries results in a single MULTIPOLYGON geometry:

ab = c(a, b)

ab
## MULTIPOLYGON (((0 0, 0 -1, 7.5 -1, 7.5 0, 0 0)), ((0 1, 1 0, 2 0.5, 3 0, 4 0, 5 0.5, 6 -0.5, 7 -0.5, 7 1, 0 1)))

class(ab)
## [1] "XY"           "MULTIPOLYGON" "sfg"

What type of geometry do you think c(a,b,pnt1) is?

Keep in mind that c always returns a single geometry, composed of all the shapes in its input. This is different from collecting the geometries into a geometry column, where the geometries are kept separate, which is done using function st_sfc as shown below (Section 7.2.3).

The multipolygon ab, which we have just created, is shown in Figure 7.10:

plot(ab, border = 'darkgreen', col = '#00FF0033', lwd = 2)

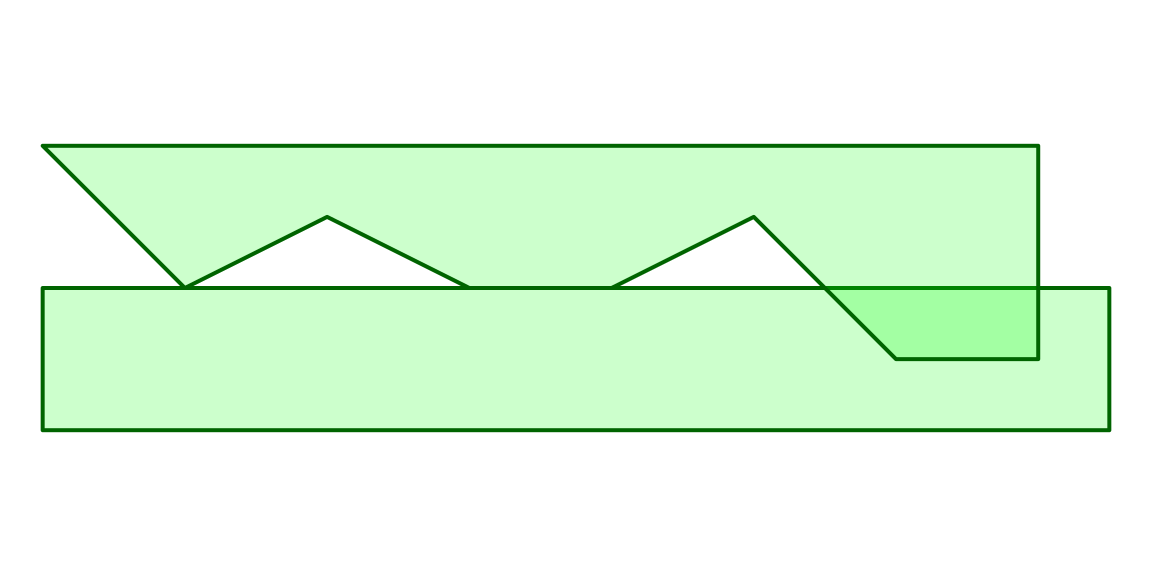
Figure 7.10: An sfg object of type MULTIPOLYGON

A new geometry can be calculated applying various functions on an existing one(s). For example, the following example calculates the intersection of a and b, which is a new geometry hereby named i. We are going to learn about st_intersection, and other geometry-generating functions, in Chapter 8.

i = st_intersection(a, b)

The result happens to be a GEOMETRYCOLLECTION, as demonstrated in Figure 7.7:

i
## GEOMETRYCOLLECTION (POLYGON ((7 0, 7 -0.5, 6 -0.5, 5.5 0, 7 0)), LINESTRING (4 0, 3 0), POINT (1 0))

class(i)
## [1] "XY"                 "GEOMETRYCOLLECTION" "sfg"

Figure 7.11 displays the GEOMETRYCOLLECTION named i:

plot(i, border = 'black', col = 'darkgrey', lwd = 2)

Figure 7.11: An sfg object of type GEOMETRYCOLLECTION

7.2.3 Geometry column (sfc)

Let’s create two more point geometries (Section 7.2.2) named pnt2 and pnt3, representing two other points:

pnt2 = st_point(c(34.812831, 31.260284))
pnt3 = st_point(c(35.011635, 31.068616))

Geometry objects (sfg) can be collected into a geometry column (sfc) object. This is done with function st_sfc.

In addition to the geometries, a geometry column object also contains a Coordinate Reference System (CRS) definition (more information on CRS is given below, in Section 7.9), specified with the crs parameter of function st_sfc. Four types of CRS definitions are accepted:

• An EPSG code (e.g., 4326)
• A crs object of another layer, as returned by st_crs
• A PROJ4 string (e.g., '+proj=longlat +datum=WGS84 +no_defs')
• A WKT string

The first two methods are the most useful ones, and we are going to use them in this book. If the crs argument is omitted, the default is to set an “undefined” CRS (i.e., NA).

Let’s combine the three POINT geometries—pnt1, pnt2 and pnt3—into a geometry column (sfc) object named geom. We will specify that the coordinates are lon/lat (WGS84), using the simplest method—an EPSG code (4326). More information on types of CRS, as well as where we can find the EPSG code of a particular CRS, is given in Section 7.9.2.

geom = st_sfc(pnt1, pnt2, pnt3, crs = 4326)

Here is a summary of the resulting geometry column:

geom
## Geometry set for 3 features 
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 34.79844 ymin: 31.06862 xmax: 35.01164 ymax: 31.26028
## Geodetic CRS:  WGS 84
## POINT (34.79844 31.24329)
## POINT (34.81283 31.26028)
## POINT (35.01163 31.06862)

The printout demostrates that other than the geometries themselves, and the derived properties of type, dimensionality, and bounding box, the geometry column contains the additional piece of information on the CRS.

The information in the geometry column, i.e., the three geometries, is shown in Figure 7.12:

plot(geom)

Figure 7.12: An sfc object with three point geometries

7.2.4 Layer (sf)

A geometry column (sfc) can be combined with non-spatial columns, also known as attributes, resulting in a layer (sf) object. In our case, the three points in the sfc geometry column geom (Section 7.2.3) represent the location of the three railway stations in Beer-Sheva and Dimona. Let’s create a data.frame with several non-spatial properties of the stations, which we already worked with in Section 4.1.2, using function data.frame (Section 4.1.2):

name = c('Beer-Sheva Center', 'Beer-Sheva University', 'Dimona')
city = c('Beer-Sheva', 'Beer-Sheva', 'Dimona')
lines = c(4, 5, 1)
piano = c(FALSE, TRUE, FALSE)
dat = data.frame(name, city, lines, piano)
dat
##                    name       city lines piano
## 1     Beer-Sheva Center Beer-Sheva     4 FALSE
## 2 Beer-Sheva University Beer-Sheva     5  TRUE
## 3                Dimona     Dimona     1 FALSE

Now, we can combine the attribute table dat (data.frame) and the geometry column geom (sfc). This is done using function st_sf, resulting in a layer (sf):

layer = st_sf(dat, geom)

Note that the order of rows in the attribute table must match the order of the geometries for this operation to make sense! Here is the resulting sf layer:

layer
## Simple feature collection with 3 features and 4 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 34.79844 ymin: 31.06862 xmax: 35.01164 ymax: 31.26028
## Geodetic CRS:  WGS 84
##                    name       city lines piano                      geom
## 1     Beer-Sheva Center Beer-Sheva     4 FALSE POINT (34.79844 31.24329)
## 2 Beer-Sheva University Beer-Sheva     5  TRUE POINT (34.81283 31.26028)
## 3                Dimona     Dimona     1 FALSE POINT (35.01163 31.06862)

7.2.5 Interactive mapping with mapview

Function mapview—which we are familiar with from Section 5.3.7.2—is useful for inspecting vector layers too. For example:

library(mapview)
mapview(layer)

---

7.3 Extracting layer components

In Section 7.2 we:

• Started from raw coordinates
• Convered them to geometry objects (sfg) using a function such as st_point, st_polygon, etc. (Section 7.2.2)
• Combined the geometries to a geometry column (sfc) using function st_sfc (Section 7.2.3)
• Added attributes to the geometry column to get a layer (sf) using function st_sf (Section 7.2.4)

which can be summarized as: coordinates → sfg → sfc → sf.

Sometimes we are interested in the opposite “direction”. In other words, we sometimes need to extract the simpler components (geometry, attributes, coordinates) from an existing layer:

• sf → geometry column (sfc)
• sf → attribute table (data.frame)
• sf → coordinates (matrix)

The geometry column (sfc) component can be extracted from an sf layer object using function st_geometry:

st_geometry(layer)
## Geometry set for 3 features 
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 34.79844 ymin: 31.06862 xmax: 35.01164 ymax: 31.26028
## Geodetic CRS:  WGS 84
## POINT (34.79844 31.24329)
## POINT (34.81283 31.26028)
## POINT (35.01163 31.06862)

The non-spatial columns of an sf layer, i.e., the attribute table, can be extracted from an sf object using function st_drop_geometry:

st_drop_geometry(layer)
##                    name       city lines piano
## 1     Beer-Sheva Center Beer-Sheva     4 FALSE
## 2 Beer-Sheva University Beer-Sheva     5  TRUE
## 3                Dimona     Dimona     1 FALSE

The latter is analogous to opening an attribute table of a vector layer in GIS software, such as ArcGIS (Figure 7.13).

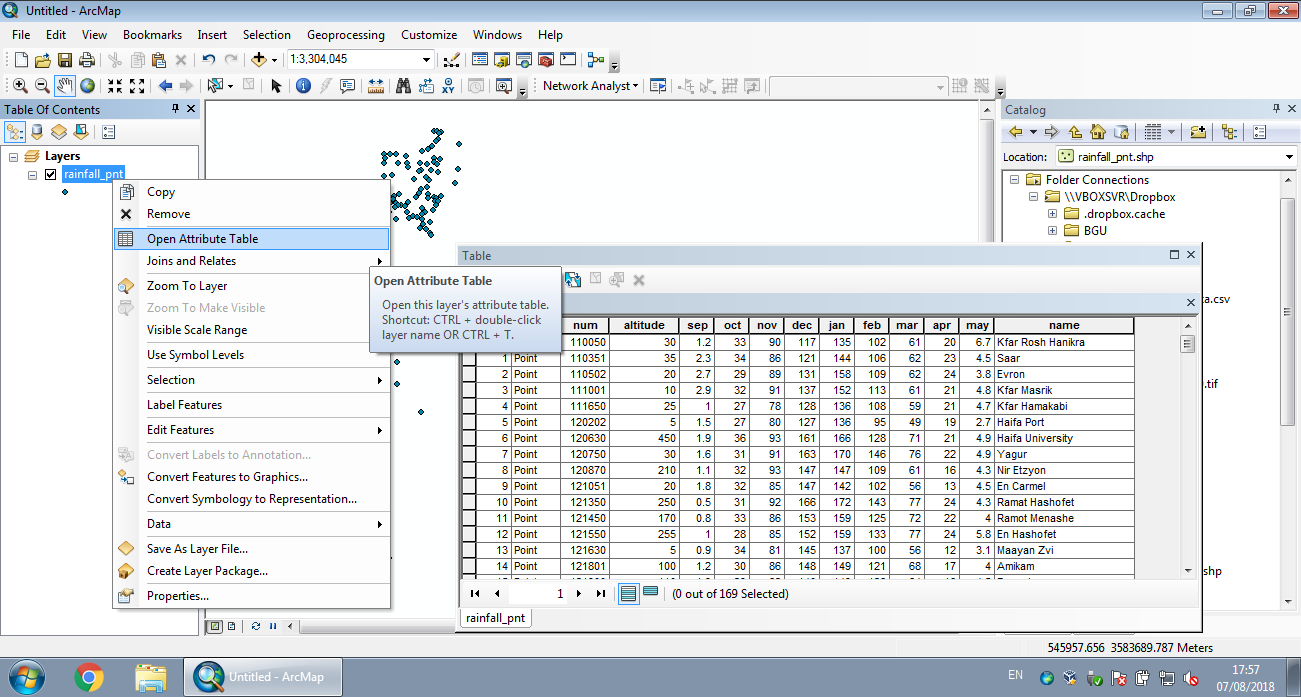
Figure 7.13: Attribute table in ArcGIS

The coordinates of sf, sfc or sfg objects can be obtained with function st_coordinates. The coordinates are returned as a matrix:

st_coordinates(layer)
##             X        Y
## [1,] 34.79844 31.24329
## [2,] 34.81283 31.26028
## [3,] 35.01163 31.06862

In the case of a two-dimensional POINT layer, which is the most common use case of st_coordinates, the returned matrix has two columns X and Y as shown above. (With other types of geometries, the matrix has additional columns containing the information on grouping of point coordinates into shapes.)

7.4 Creating point layer from table

A common way of creating a point layer is to transform a table which has X and Y coordinate columns. Function st_as_sf can transform a table (data.frame) into a point layer (sf). In st_as_sf we specify:

• x—The data.frame to be converted
• coords—Columns names with the coordinates (X, Y)
• crs—The CRS (NA if left unspecified)

Let’s take the rainfall.csv table as an example. The rainfall.csv table contains two columns named x_utm and y_utm which we have not worked with until now. These two columns contain the meteorological station coordinates in the UTM 36N CRS (EPSG code 32636):

rainfall = read.csv('data/rainfall.csv')
head(rainfall)
##      num altitude sep oct nov dec jan feb mar apr may              name
## 1 110050       30 1.2  33  90 117 135 102  61  20 6.7 Kfar Rosh Hanikra
## 2 110351       35 2.3  34  86 121 144 106  62  23 4.5              Saar
## 3 110502       20 2.7  29  89 131 158 109  62  24 3.8             Evron
## 4 111001       10 2.9  32  91 137 152 113  61  21 4.8       Kfar Masrik
## 5 111650       25 1.0  27  78 128 136 108  59  21 4.7     Kfar Hamakabi
## 6 120202        5 1.5  27  80 127 136  95  49  19 2.7        Haifa Port
##      x_utm   y_utm
## 1 696533.1 3660837
## 2 697119.1 3656748
## 3 696509.3 3652434
## 4 696541.7 3641332
## 5 697875.3 3630156
## 6 687006.2 3633330

Accordingly, the rainfall table can be converted to an sf layer using st_as_sf as follows:

rainfall = st_as_sf(rainfall, coords = c('x_utm', 'y_utm'), crs = 32636)

Note that:

• The coords column names correspond to X and Y, in that order! Using the reverse order, as in coords=c('y_utm','x_utm'), would be incorrect.
• 32636 is the EPSG code of the UTM 36N projection (Table 7.4)

The analogous operation in ArcGIS is the Display XY Data menu (Figures 7.14–7.16).

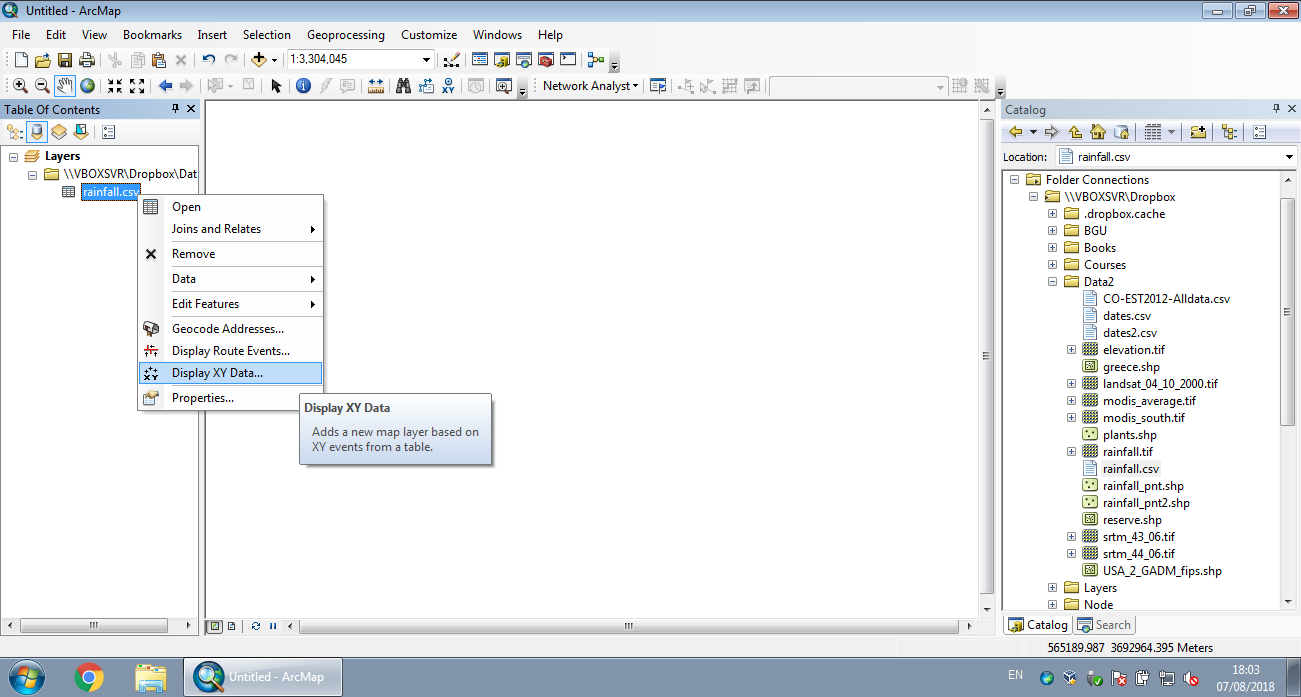
Figure 7.14: Displaying XY data from CSV in ArcGIS (Step 1)

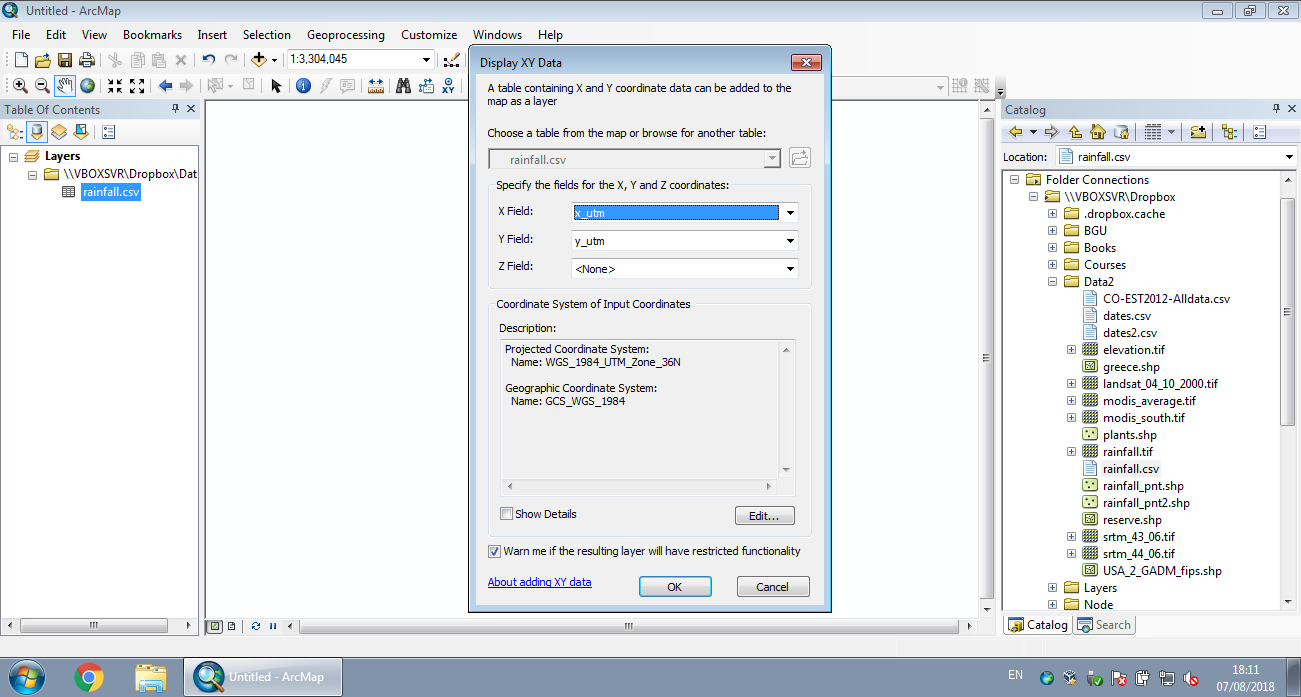
Figure 7.15: Displaying XY data from CSV in ArcGIS (Step 2)

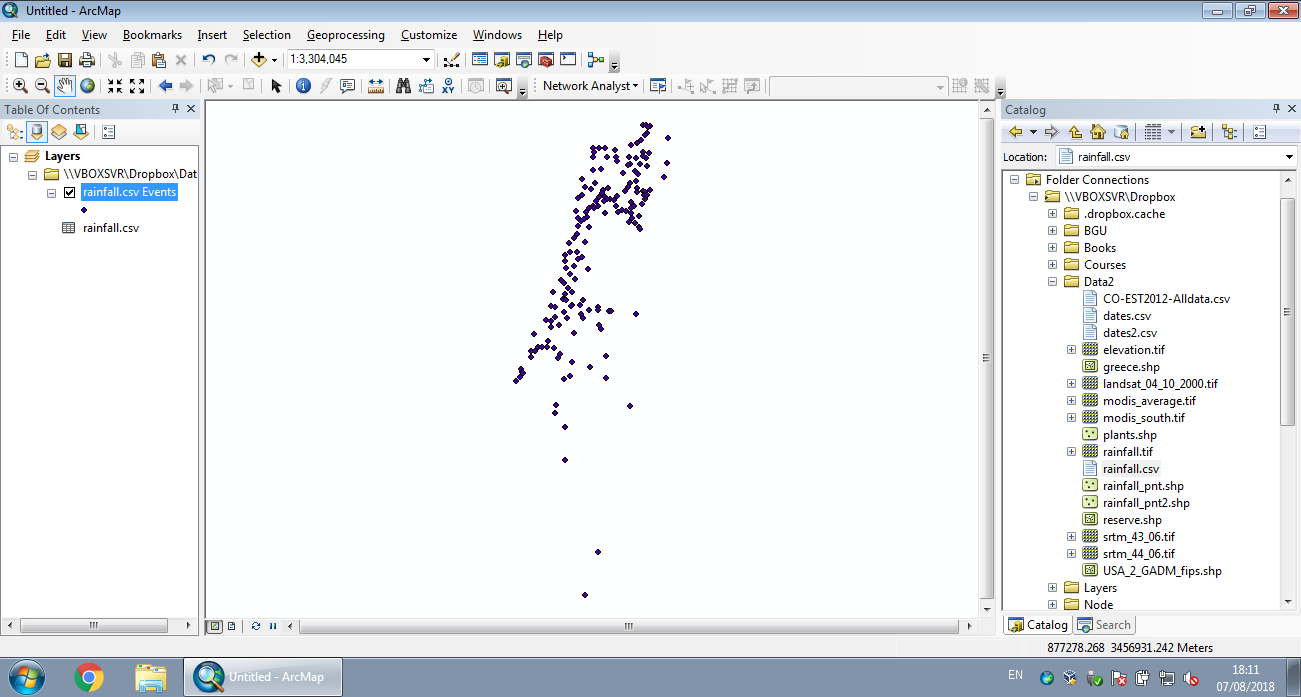
Figure 7.16: Displaying XY data from CSV in ArcGIS (Step 3)

Here is the resulting sf layer:

rainfall
## Simple feature collection with 169 features and 12 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 629301.4 ymin: 3270290 xmax: 761589.2 ymax: 3681163
## Projected CRS: WGS 84 / UTM zone 36N
## First 10 features:
##       num altitude sep oct nov dec jan feb mar apr may              name
## 1  110050       30 1.2  33  90 117 135 102  61  20 6.7 Kfar Rosh Hanikra
## 2  110351       35 2.3  34  86 121 144 106  62  23 4.5              Saar
## 3  110502       20 2.7  29  89 131 158 109  62  24 3.8             Evron
## 4  111001       10 2.9  32  91 137 152 113  61  21 4.8       Kfar Masrik
## 5  111650       25 1.0  27  78 128 136 108  59  21 4.7     Kfar Hamakabi
## 6  120202        5 1.5  27  80 127 136  95  49  19 2.7        Haifa Port
## 7  120630      450 1.9  36  93 161 166 128  71  21 4.9  Haifa University
## 8  120750       30 1.6  31  91 163 170 146  76  22 4.9             Yagur
## 9  120870      210 1.1  32  93 147 147 109  61  16 4.3        Nir Etzyon
## 10 121051       20 1.8  32  85 147 142 102  56  13 4.5         En Carmel
##                    geometry
## 1  POINT (696533.1 3660837)
## 2  POINT (697119.1 3656748)
## 3  POINT (696509.3 3652434)
## 4  POINT (696541.7 3641332)
## 5  POINT (697875.3 3630156)
## 6  POINT (687006.2 3633330)
## 7  POINT (689553.7 3626282)
## 8  POINT (694694.5 3624388)
## 9  POINT (686489.5 3619716)
## 10 POINT (683148.4 3616846)

An interactive map, showing the spatial locations of the rainfall stations, can be created using mapview (Section 7.2.5). Here, we are using the additional zcol parameter to choose which attribute will be used for the color scale:

mapview(rainfall, zcol = 'jan')

---

7.5 sf layer properties

7.5.1 Dimensions

An sf layer is basically a special type of data.frame, where one of the columns is a geometry column. Therefore, many of the functions we learned when working with data.frame tables (Chapter 4) also work on sf layers.

For example, we can get the number of rows, or features, with nrow:

nrow(rainfall)
## [1] 169

and the number of columns (including the geometry column) with ncol:

ncol(rainfall)
## [1] 13

or both with dim:

dim(rainfall)
## [1] 169  13

What is the result of st_geometry(rainfall)? st_drop_geometry(rainfall)?

7.5.2 Spatial properties

The st_bbox function returns the bounding box coordinates, just like for stars objects (Section 5.3.8.3):

st_bbox(rainfall)
##      xmin      ymin      xmax      ymax 
##  629301.4 3270290.2  761589.2 3681162.7

The st_crs function returns the Coordinate Reference System (CRS), also the same way as for stars objects (Section 5.3.8.3):

st_crs(rainfall)
## Coordinate Reference System:
##   User input: EPSG:32636 
##   wkt:
## PROJCRS["WGS 84 / UTM zone 36N",
##     BASEGEOGCRS["WGS 84",
##         ENSEMBLE["World Geodetic System 1984 ensemble",
##             MEMBER["World Geodetic System 1984 (Transit)"],
##             MEMBER["World Geodetic System 1984 (G730)"],
##             MEMBER["World Geodetic System 1984 (G873)"],
##             MEMBER["World Geodetic System 1984 (G1150)"],
##             MEMBER["World Geodetic System 1984 (G1674)"],
##             MEMBER["World Geodetic System 1984 (G1762)"],
##             MEMBER["World Geodetic System 1984 (G2139)"],
##             ELLIPSOID["WGS 84",6378137,298.257223563,
##                 LENGTHUNIT["metre",1]],
##             ENSEMBLEACCURACY[2.0]],
##         PRIMEM["Greenwich",0,
##             ANGLEUNIT["degree",0.0174532925199433]],
##         ID["EPSG",4326]],
##     CONVERSION["UTM zone 36N",
##         METHOD["Transverse Mercator",
##             ID["EPSG",9807]],
##         PARAMETER["Latitude of natural origin",0,
##             ANGLEUNIT["degree",0.0174532925199433],
##             ID["EPSG",8801]],
##         PARAMETER["Longitude of natural origin",33,
##             ANGLEUNIT["degree",0.0174532925199433],
##             ID["EPSG",8802]],
##         PARAMETER["Scale factor at natural origin",0.9996,
##             SCALEUNIT["unity",1],
##             ID["EPSG",8805]],
##         PARAMETER["False easting",500000,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8806]],
##         PARAMETER["False northing",0,
##             LENGTHUNIT["metre",1],
##             ID["EPSG",8807]]],
##     CS[Cartesian,2],
##         AXIS["(E)",east,
##             ORDER[1],
##             LENGTHUNIT["metre",1]],
##         AXIS["(N)",north,
##             ORDER[2],
##             LENGTHUNIT["metre",1]],
##     USAGE[
##         SCOPE["Engineering survey, topographic mapping."],
##         AREA["Between 30°E and 36°E, northern hemisphere between equator and 84°N, onshore and offshore. Belarus. Cyprus. Egypt. Ethiopia. Finland. Israel. Jordan. Kenya. Lebanon. Moldova. Norway. Russian Federation. Saudi Arabia. Sudan. Syria. Turkey. Uganda. Ukraine."],
##         BBOX[0,30,84,36]],
##     ID["EPSG",32636]]

Question: what is the difference between the two plots in Figure 7.17, created using the following expressions?

plot(st_geometry(rainfall))
plot(st_coordinates(rainfall)[, 1], st_coordinates(rainfall)[, 2])

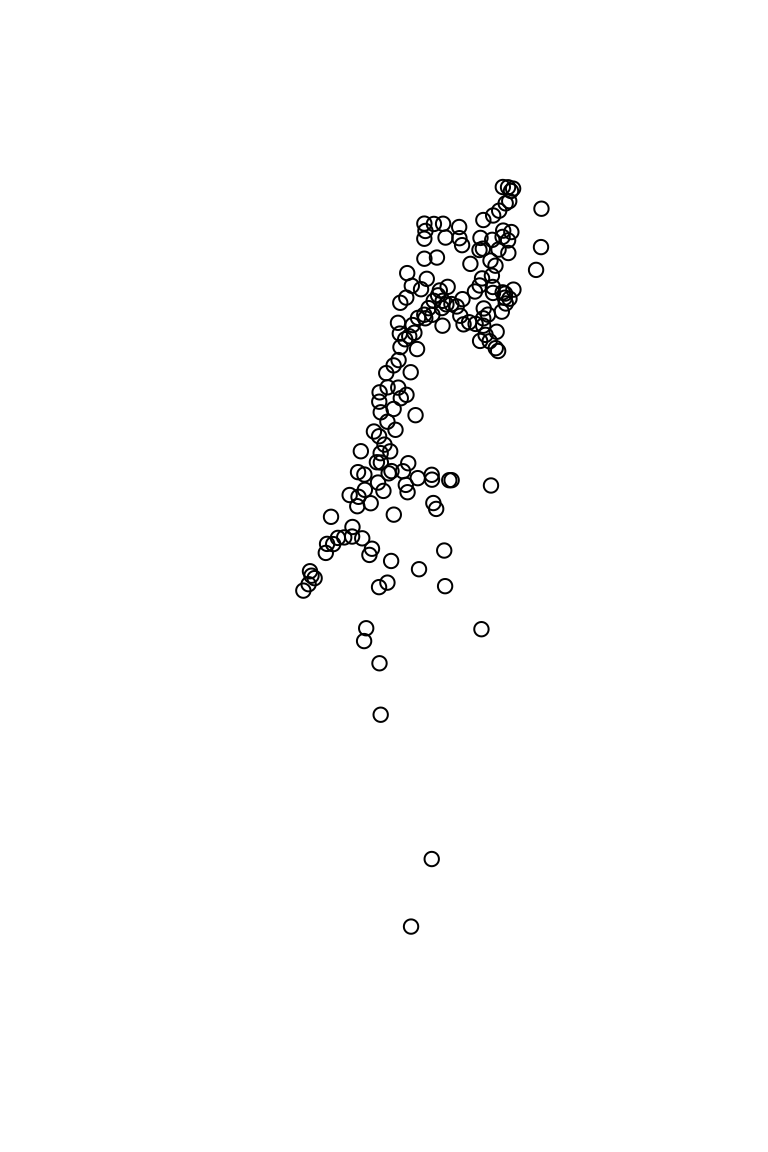
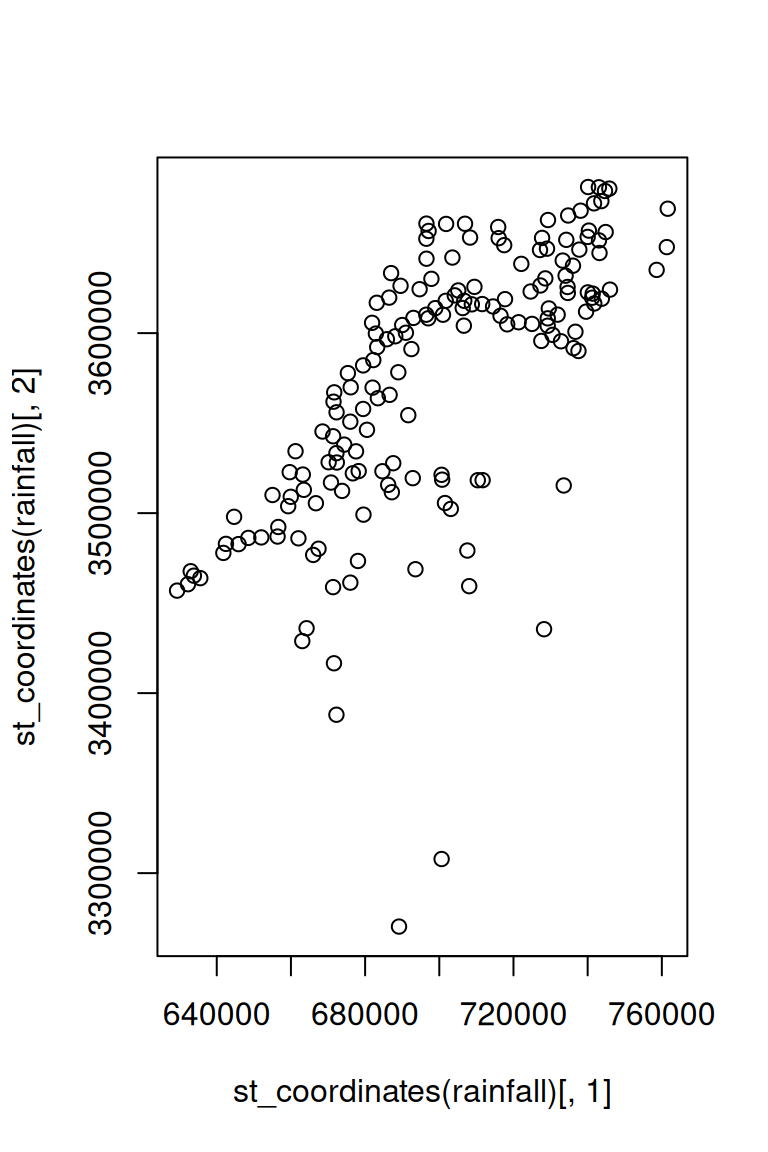
Figure 7.17: Two plots

7.6 Subsetting based on attributes

Subsetting of features in an sf vector layer is exactly the same as filtering rows in a data.frame (Section 4.1.5). Remember: an sf layer is a data.frame. For example, the following expressions subset the rainfall layer:

rainfall[1:10, ]
rainfall[rainfall$jan > 100, ]

Which meteorological stations are being selected in each of these two expressions?

Figure 7.18 shows the resulting subsets:

plot(st_geometry(rainfall[1:10, ]), main = 'rainfall[1:10, ]')
plot(st_geometry(rainfall[rainfall$jan > 100, ]), main = 'rainfall[rainfall$jan > 100, ]')

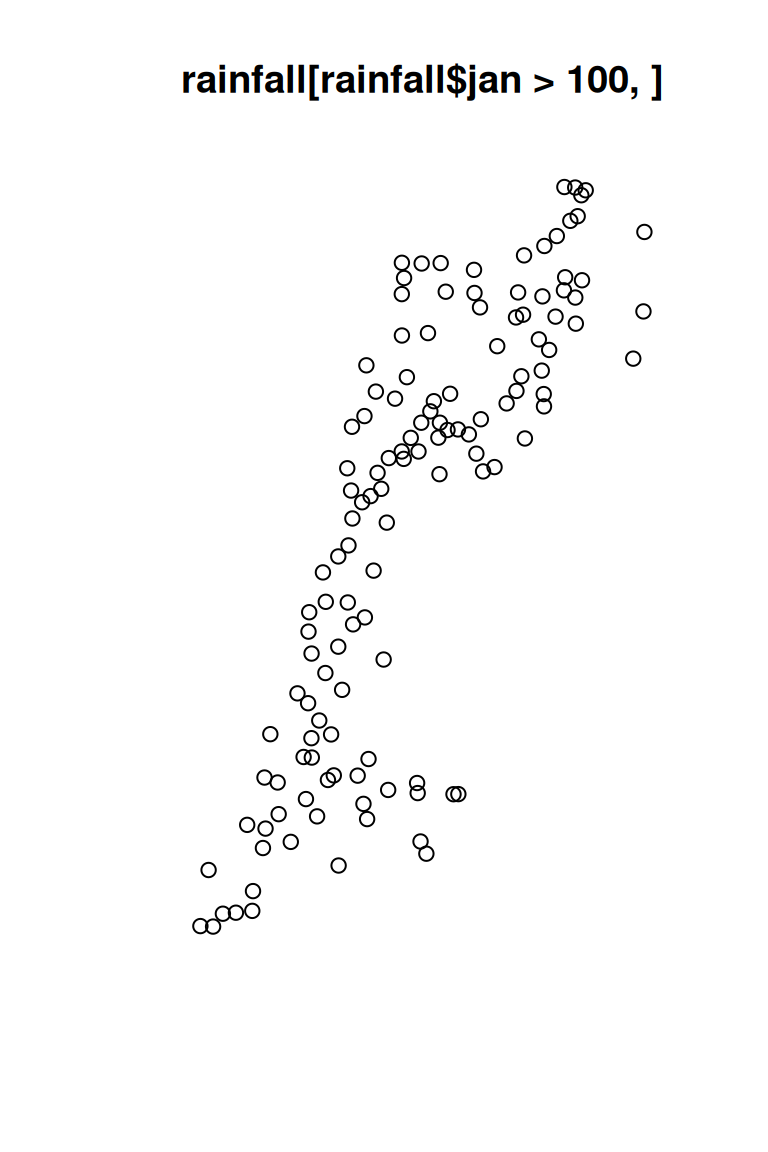
Figure 7.18: Subsets of the rainfall layer

Subsetting columns in sf is also similar to subsetting columns in a data.frame, with one exception: the geometry column. The geometry column “sticks” to the subset, by default, even if we do not explicitly select it, so that the resulting subset remains an sf object:

rainfall[1:5, c('jan', 'feb')]
## Simple feature collection with 5 features and 2 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 696509.3 ymin: 3630156 xmax: 697875.3 ymax: 3660837
## Projected CRS: WGS 84 / UTM zone 36N
##   jan feb                 geometry
## 1 135 102 POINT (696533.1 3660837)
## 2 144 106 POINT (697119.1 3656748)
## 3 158 109 POINT (696509.3 3652434)
## 4 152 113 POINT (696541.7 3641332)
## 5 136 108 POINT (697875.3 3630156)

In case we do need to omit the geometry column, and get a data.frame, we have to apply st_drop_geometry (Section 7.3) on the subset:

st_drop_geometry(rainfall[1:5, c('jan', 'feb')])
##   jan feb
## 1 135 102
## 2 144 106
## 3 158 109
## 4 152 113
## 5 136 108

7.7 Reading vector layers

In addition to creating from raw coordinates (Section 7.2) and transforming a data.frame to point layer (Section 7.4), we often create vector layers by reading from a file or from a spatial database (Section 7.1.2)²⁹. Reading a vector layer from a file or a database is done using the st_read function.

For example, the following expression reads the Shapefile of US county boundaries, named USA_2_GADM_fips.shp, from the course materials. Note that in the case of the Shapefile file format, the path to just the .shp file needs to be specified, even though the Shapefile is composed of several files placed together (Table 7.1):

county = st_read('data/USA_2_GADM_fips.shp', quiet = TRUE)
county
## Simple feature collection with 3103 features and 4 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -124.7628 ymin: 24.52042 xmax: -66.94889 ymax: 49.3833
## Geodetic CRS:  WGS 84
## First 10 features:
##         NAME_1     NAME_2 TYPE_2  FIPS                       geometry
## 1  Connecticut Litchfield County 09005 MULTIPOLYGON (((-73.05166 4...
## 2  Connecticut   Hartford County 09003 MULTIPOLYGON (((-72.50941 4...
## 3  Connecticut    Tolland County 09013 MULTIPOLYGON (((-72.13582 4...
## 4  Connecticut    Windham County 09015 MULTIPOLYGON (((-71.79794 4...
## 5   California   Siskiyou County 06093 MULTIPOLYGON (((-122.2873 4...
## 6   California  Del Norte County 06015 MULTIPOLYGON (((-124.2492 4...
## 7   California      Modoc County 06049 MULTIPOLYGON (((-120.0003 4...
## 8  Connecticut New London County 09011 MULTIPOLYGON (((-72.225 41....
## 9  Connecticut  Fairfield County 09001 MULTIPOLYGON (((-73.65778 4...
## 10 Connecticut  Middlesex County 09007 MULTIPOLYGON (((-72.47361 4...

The quiet=TRUE part is used to omit the layer details printout when reading. Let’s also read a GeoJSON file with the location of three particular airports in New Mexico:

airports = st_read('data/airports.geojson', quiet = TRUE)
airports
## Simple feature collection with 3 features and 1 field
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: -106.7947 ymin: 35.04807 xmax: -106.0892 ymax: 35.61621
## Geodetic CRS:  WGS 84
##                        name                   geometry
## 1 Albuquerque International POINT (-106.6169 35.04807)
## 2           Double Eagle II POINT (-106.7947 35.15559)
## 3        Santa Fe Municipal POINT (-106.0892 35.61621)

7.8 Basic plotting

When plotting an sf object with plot, we get multiple small maps—one map for each attribute. This can be useful to quickly examine the types of spatial variation in our data. For example (Figure 7.19):

plot(county)

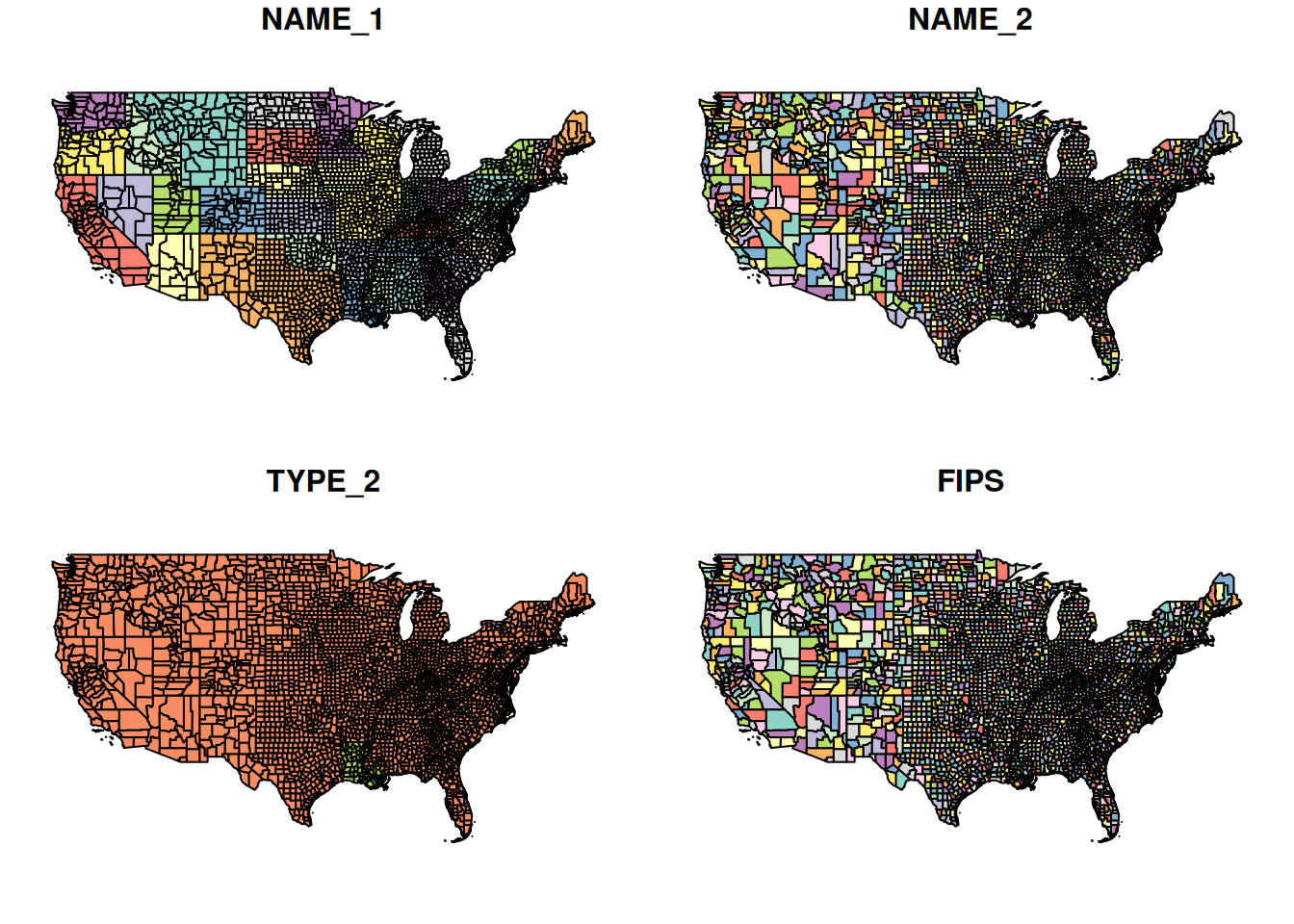
Figure 7.19: Plot of sf object

Plotting a single attribute adds a legend (Figure 7.20). The key.width and key.pos let us control the amount of space the legend takes and its placement, respectively:

plot(county[, 'TYPE_2'], key.width = lcm(5), key.pos = 4)

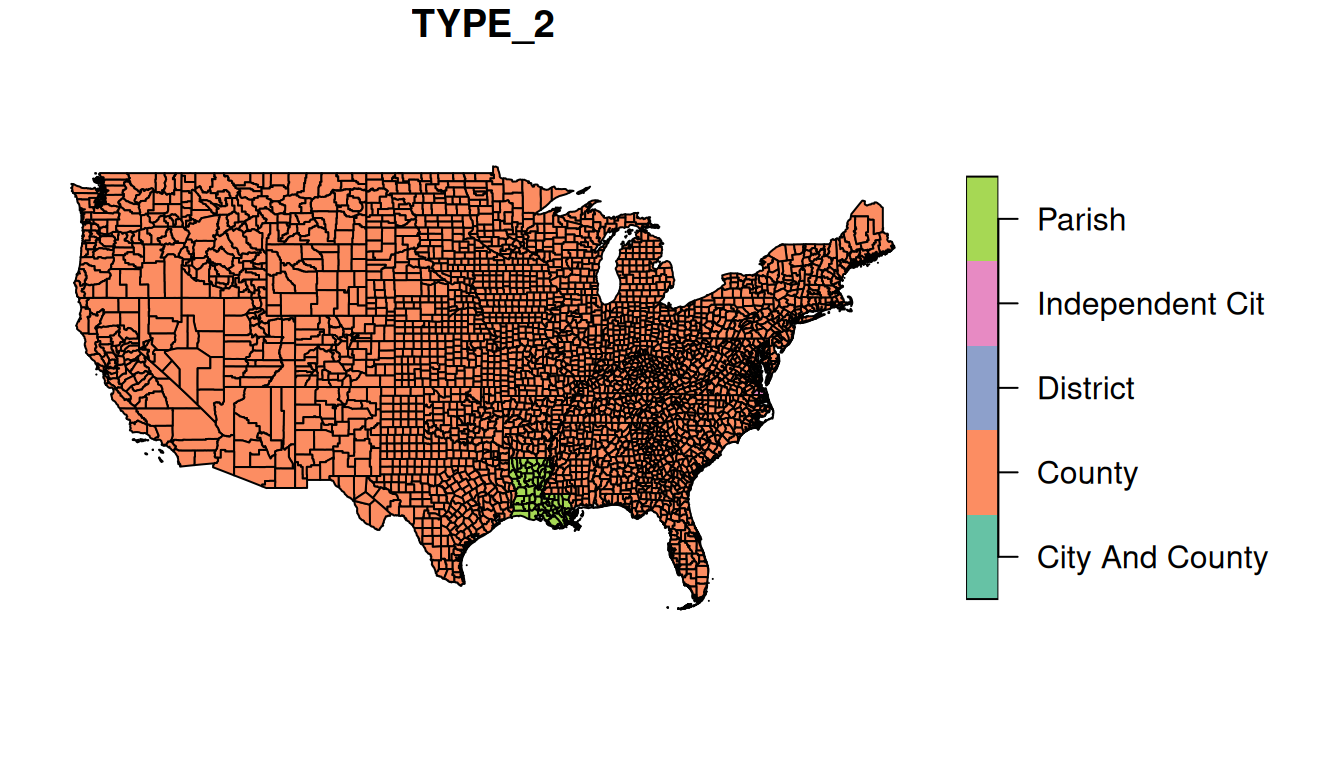
Figure 7.20: Plot of sf object, single attribute with legend

Plotting an sfc or an sfg object shows just the geometry (Figure 7.21):

plot(st_geometry(county))

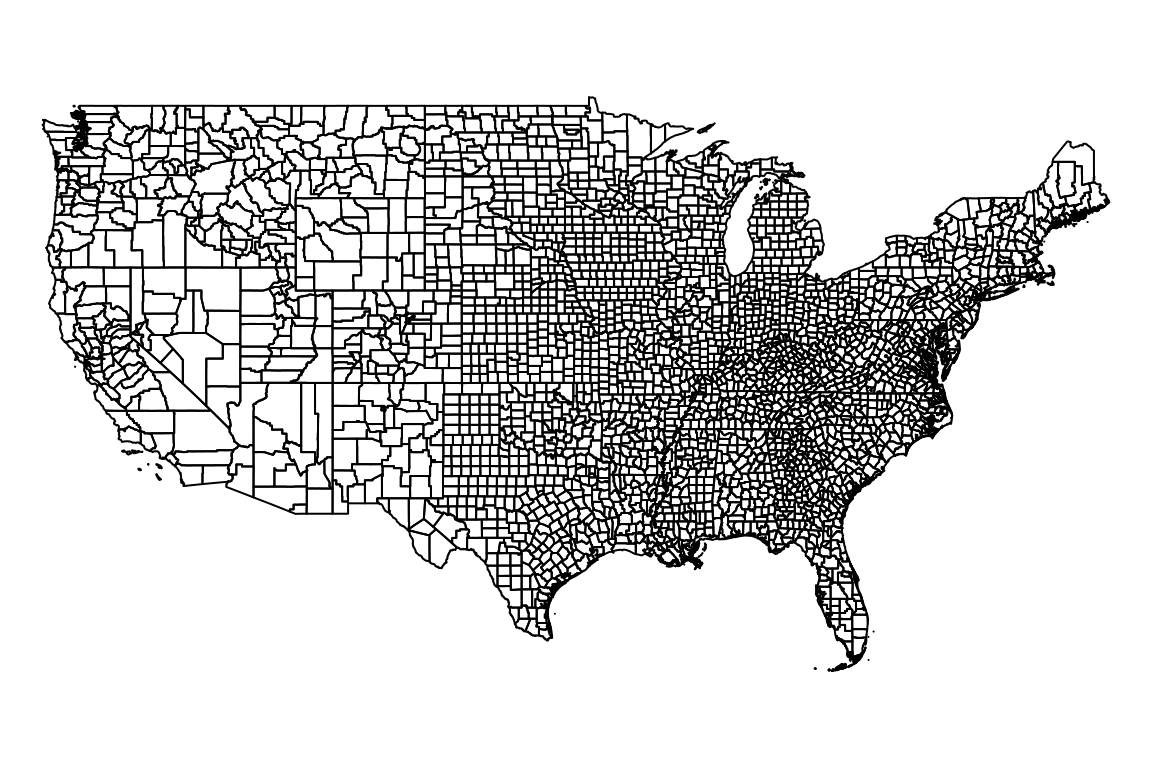
Figure 7.21: Plot of sfc object

We can use graphical parameters to control the appearance of plotted geometries, such as:

• col—Fill color
• border—Outline color
• pch—Point shape
• cex—Point size

For example, the following expression draws county borders in grey (Figure 7.22):

plot(st_geometry(county), border = 'grey')

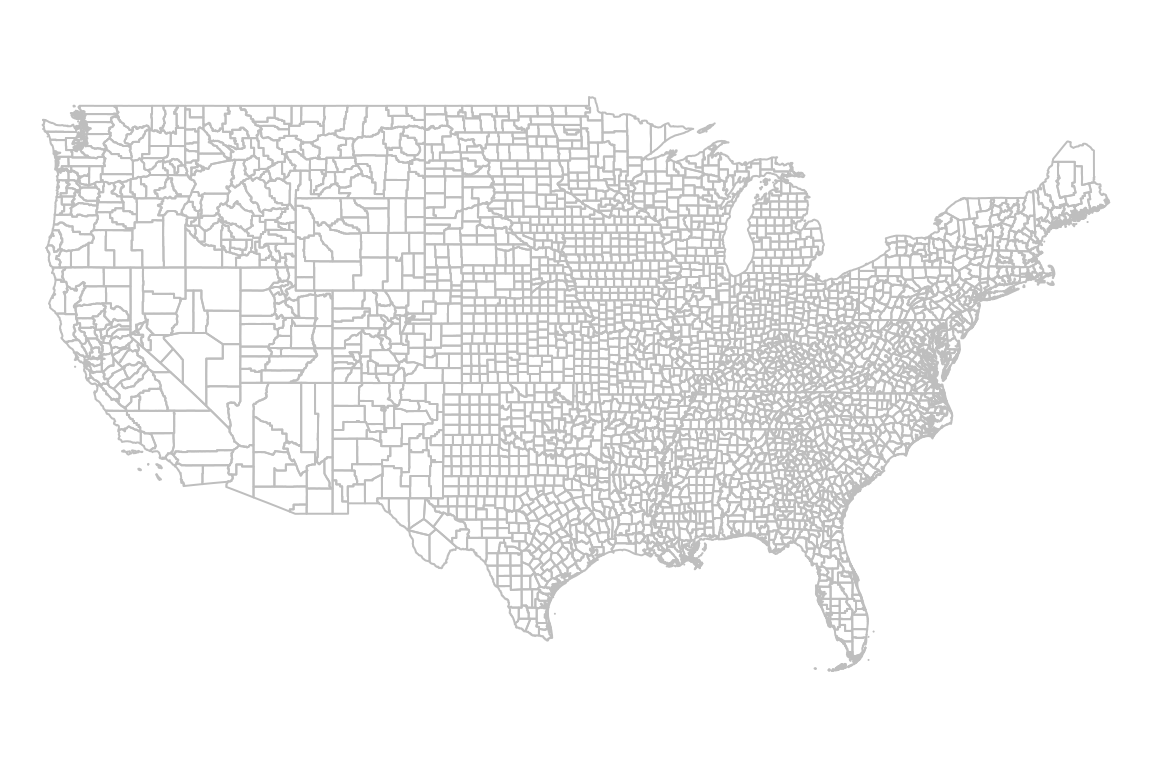
Figure 7.22: Basic plot of sfc object

Additional vector layers can be drawn in an existing graphical window using add=TRUE, similarly to the concept of layers in GIS software. For example, the following expressions draw both county and airports geometries (Figure 7.23). Note how the second expression uses add=TRUE:

plot(st_geometry(county), border = 'grey')
plot(st_geometry(airports), col = 'red', add = TRUE)

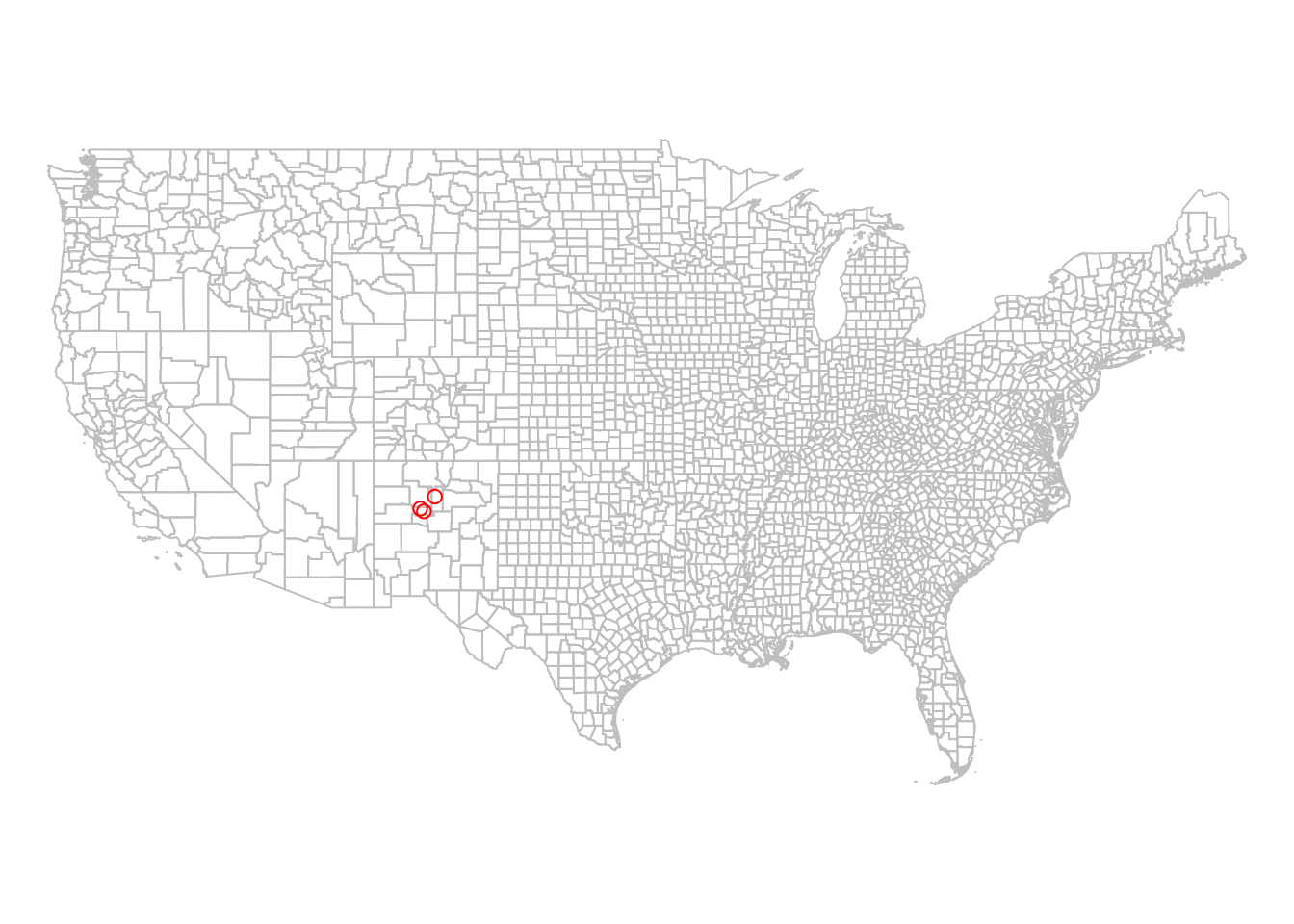
Figure 7.23: Using add=TRUE in plot

Note that all layers being plotted together need to be in the same CRS (Section 7.5.2). Otherwise, the plot will be incorrect. In case the layers are not in the same CRS, we need to reproject them to a common CRS, which we learn how to do in Section 7.9.2.

We can also use add=TRUE to combine sfg or sfc geometries with rasters in the same plot. This is often useful to examine the spatial relationship or alignment between two (or more) layers. For example, let’s plot the rainfall layer on top of the rainfall.tif raster, which is an interpolated rainfall surface we met in Chapter 1. First we will read the raster file:

library(stars)
r = read_stars('data/rainfall.tif')
names(r) = 'rainfall'

and then plot both layers (Figure 7.24):

plot(r, breaks = 'equal', col = hcl.colors(11, 'Spectral'), reset = FALSE)
plot(st_geometry(rainfall), add = TRUE)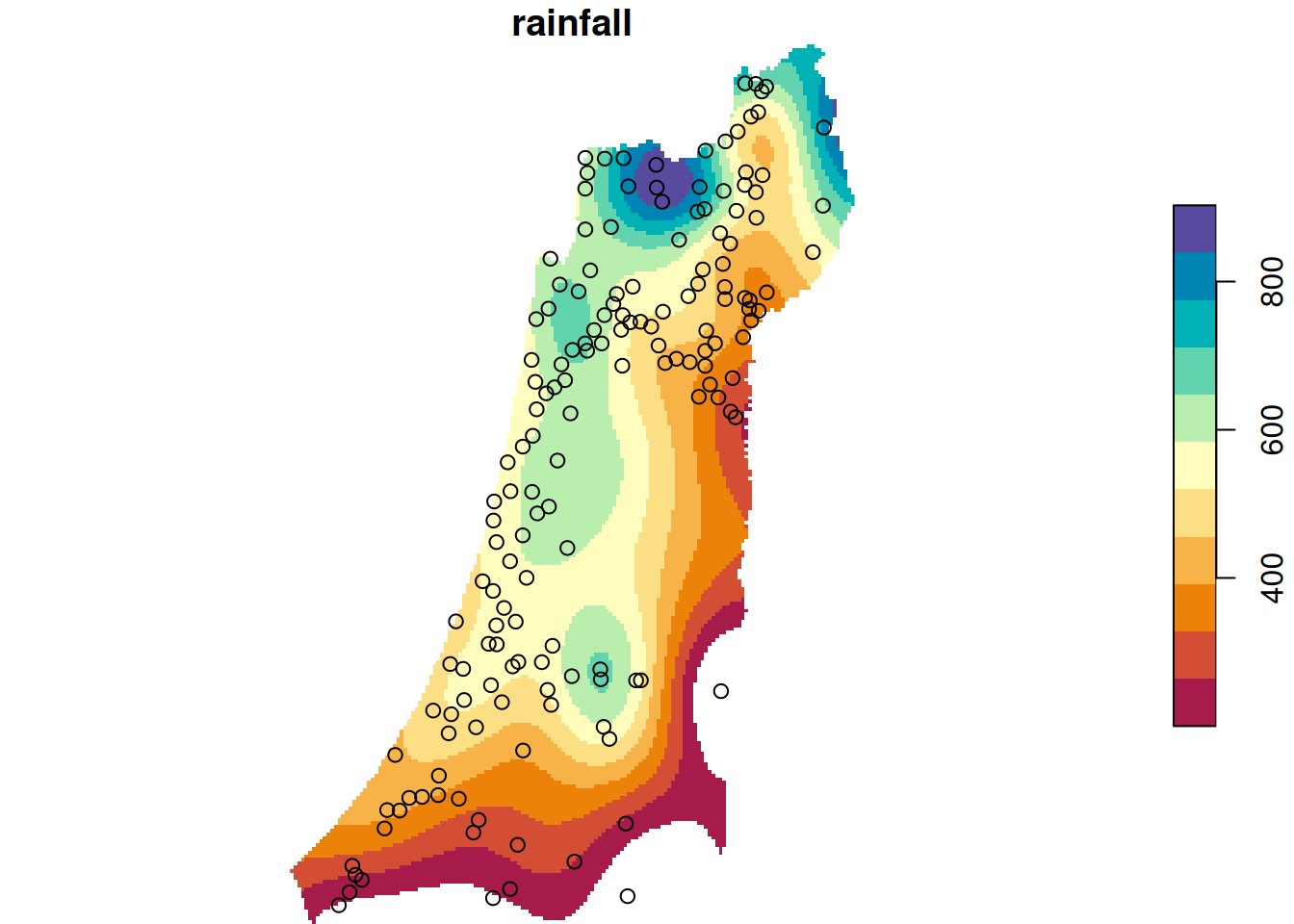

Figure 7.24: sfc layer on top of a raster

Note that we need to use the additional argument reset=FALSE whenever we are adding more layers to a stars raster plot.

7.9 Coordinate Reference Systems (CRS)

7.9.1 What are CRS?

A Coordinate Reference System (CRS) defines how the coordinates in our geometries relate to the surface of the Earth. There are two main types of CRS:

• Geographic—longitude and latitude, in degrees
• Projected—implying flat surface, usually in units of true distance (e.g., meters)

For example, Figure 7.25 shows the same polygonal layer (U.S. counties) in two different projection. On the left, the county layer is in the WGS84 geographic projection. Indeed, we can see that the axes are given in degrees of longitude and latitude. For example, we can see how the nothern border of U.S. follows the 49° latitude line. On the right, the same layer is displayed in the US National Atlas projection, where units are arbitrary but reflect true distance (meters). For example, the distance between every two consecutive grid lines is \(1000000\) \(m\) or \(1000\) \(km\).

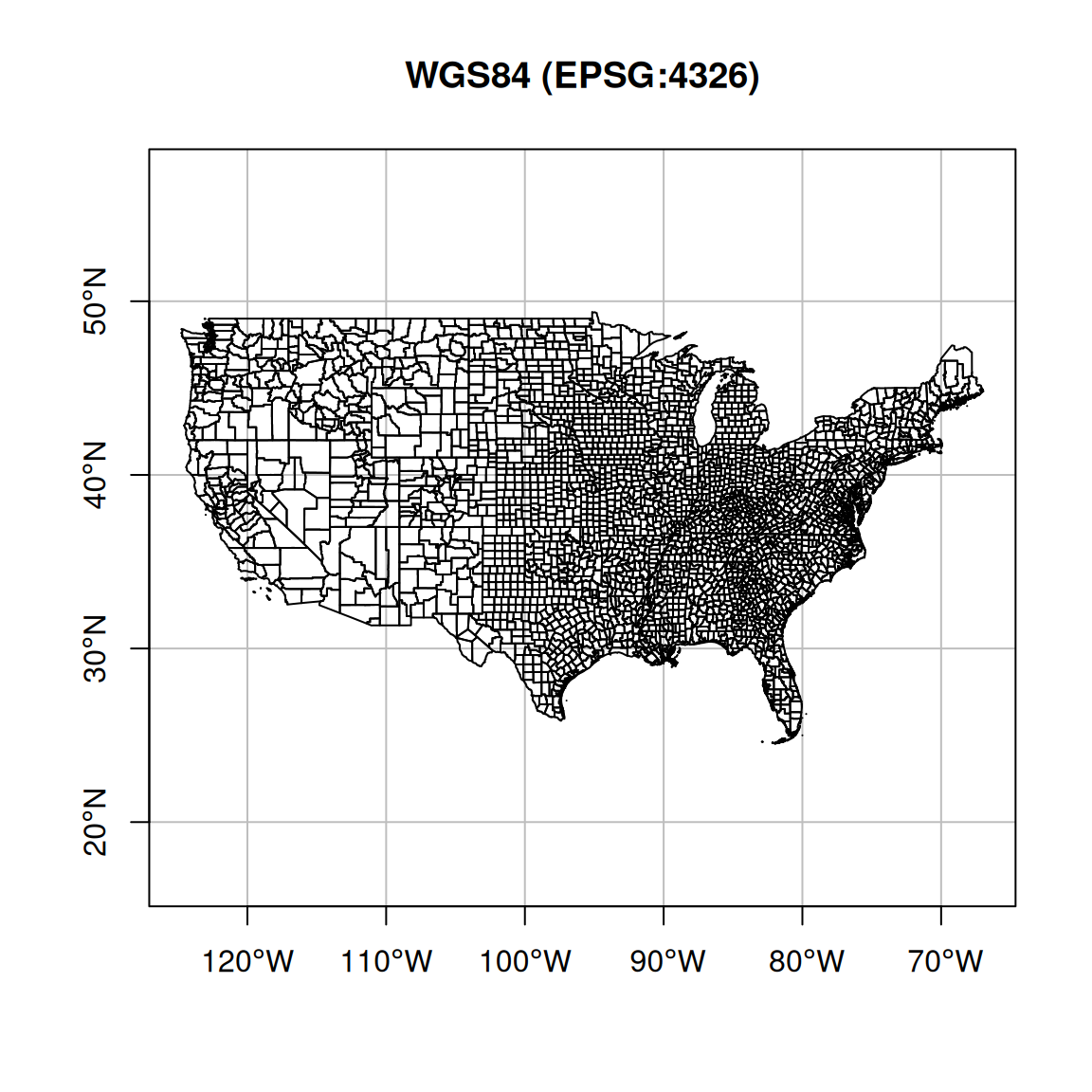
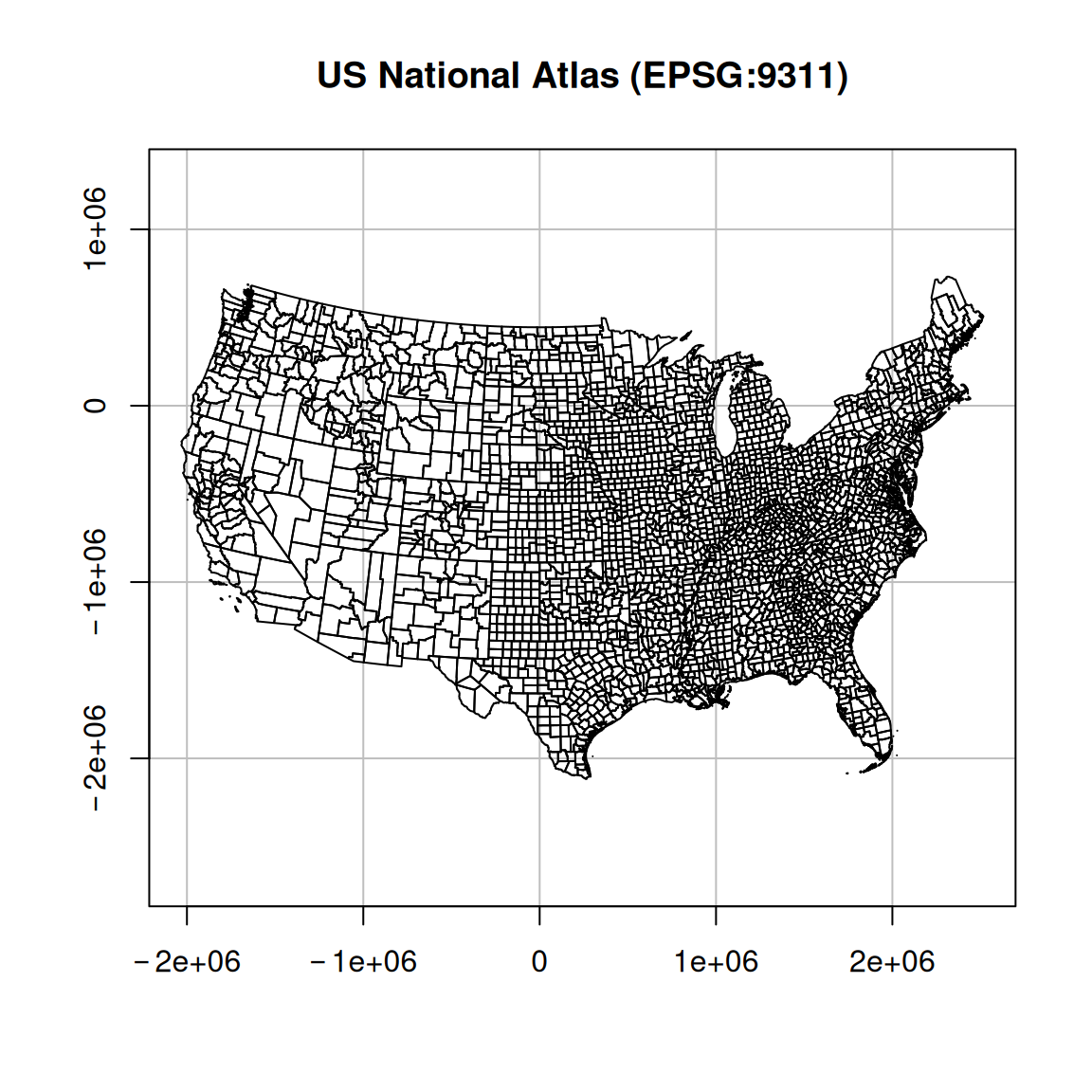
Figure 7.25: US counties in WGS84 and US Atlas projections

7.9.2 Vector layer reprojection

Reprojection is the transformation of geometry coordinates from one CRS to another. Reprojection is an important part of spatial analysis workflow, since we often need to:

• Transform several layers into the same projection, so that they can be displayed one on top of the other (e.g., Figure 7.23), or so that they can be subject to a spatial operator (e.g., Figure 7.7)
• Switch between geographic and projected CRS. For example, a geographic CRS is useful to store and publish global data, while a projected CRS is useful when we need to map local data, or to apply geometric operators such as distance measurement

A vector layer can be reprojected with st_transform. The st_transform function has two important parameters:

• x—The layer to be reprojected
• crs—The target CRS

Why don’t we need to specify the origin CRS in st_transform?

As mentioned above, the CRS can be specified in one of four ways, using an EPSG code, a crs object, a PROJ4 string, or a WKT string (Section 7.2.3). Where can we find EPSG codes, or WKT strings, of different projections? We can use CRS databases on the internet, such as http://spatialreference.org or https://epsg.io, to look up CRS definitions for a given country, of CRS name, using the search box.

In this book, we are going to encounter five different projections: WGS84, Sinusoidal, UTM 36N, ITM, and US National Atlas (Table 7.4). We are going to specify them (e.g., in st_transform) using their EPSG codes wherever possible, since this is the easiest method.

Table 7.4: Projections used in this book

Name	Type	Area	Units	EPSG code
WGS84	Geographic	World	degrees	4326
Sinusoidal	Projected	World	meters	-
UTM 36N	Projected	Israel	meters	32636
ITM	Projected	Israel	meters	2039
US National Atlas	Projected	USA	meters	9311

Now, let’s see how we can use the st_transform function to reproject layers, in practice. The county and airports are currently in WGS84 (EPSG:4326) (How can we check?). Suppose that we would like to reproject those layers to the the US National Atlas Equal Area projection (EPSG:9311). The following expressions implement the reprojection:

county = st_transform(county, 9311)
airports = st_transform(airports, 9311)

The modified layers are shown in Figure 7.26. We can clearly see that the layer orientation has changed (also see Figure 7.25).

plot(st_geometry(county), border = 'grey')
plot(st_geometry(airports), col = 'red', add = TRUE)

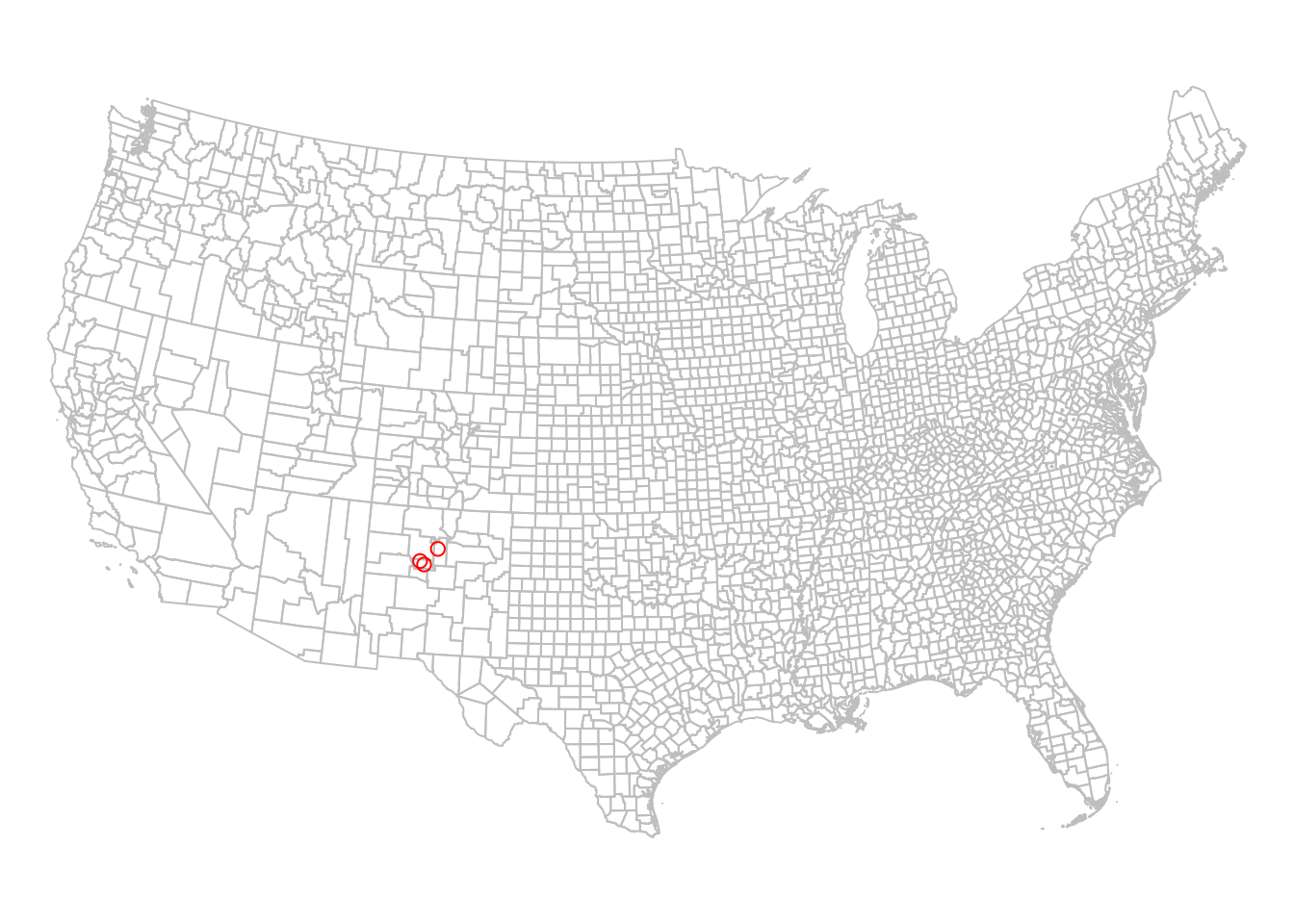
Figure 7.26: The county and airports layers in the US National Atlas Projection (EPSG=9311)

Examining the layer coordinates shows that, indeed, they have changed:

st_coordinates(st_transform(airports, 4326))  # WGS84 coordinates
##              X        Y
## [1,] -106.6169 35.04807
## [2,] -106.7947 35.15559
## [3,] -106.0892 35.61621

st_coordinates(st_transform(airports, 9311))  # US National Atlas coordinates
##              X        Y
## [1,] -605057.1 -1080157
## [2,] -620409.7 -1067009
## [3,] -552795.4 -1021040

Create a subset of county with the counties of New Mexico, Arizona and Texas only, and plot the result (Figure 7.27).

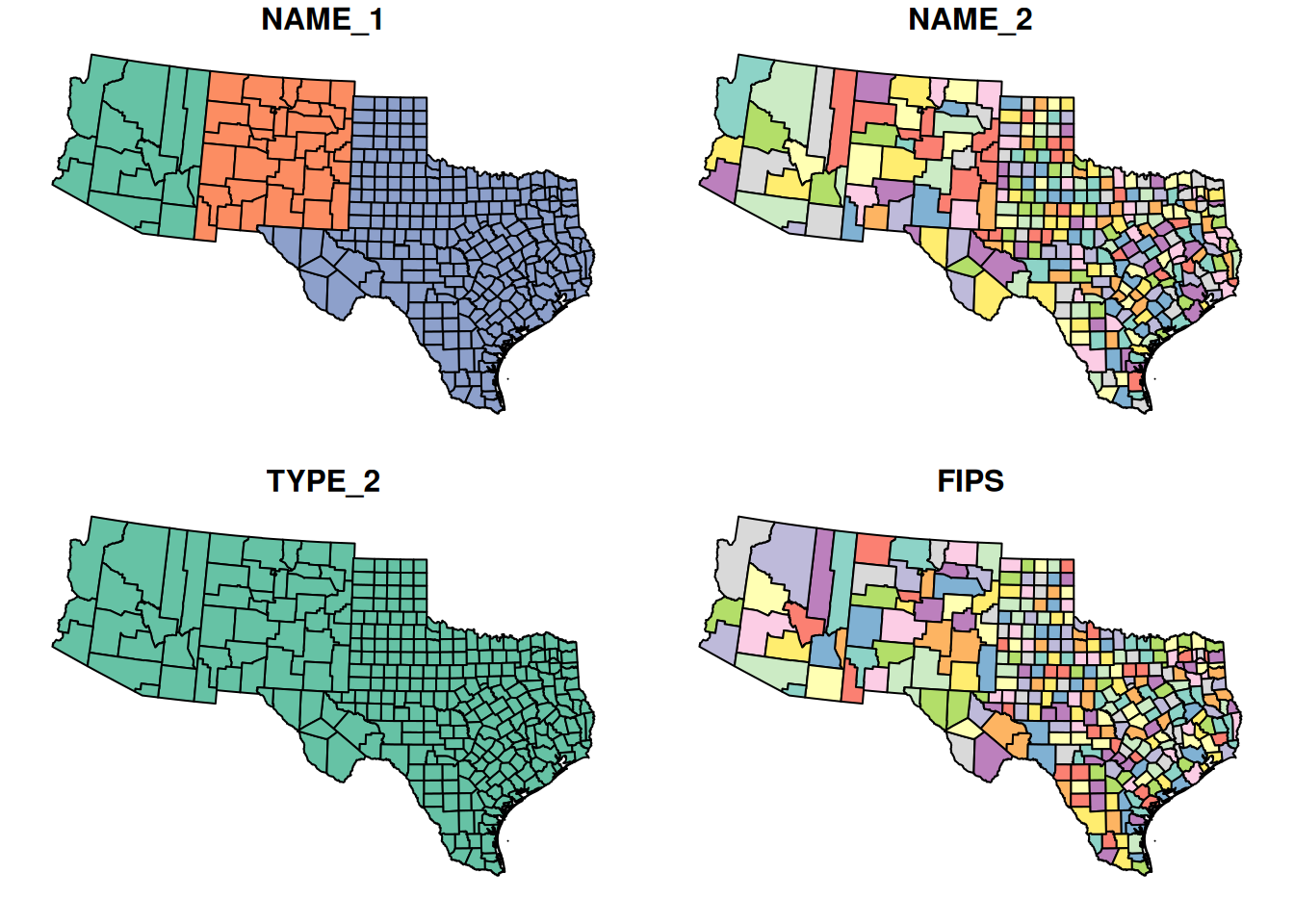
Figure 7.27: Subset of three states from the county layer

7.10 Writing vector layers

Writing an sf object to a file can be done with st_write. Before writing the rainfall layer to disk, let’s calculate a new column called annual with the annual rainfall (Section 4.5):

m = c('sep', 'oct', 'nov', 'dec', 'jan', 'feb', 'mar', 'apr', 'may')
rainfall$annual = apply(st_drop_geometry(rainfall[, m]), 1, sum)

In the last expression, why did we use st_drop_geometry(rainfall[,m]) as the first argument in apply, instead of rainfall[,m]?

The sf object can be written to a Shapefile with st_write, as follows:

st_write(rainfall, 'rainfall_pnt.shp')

The format is automatically determined based on the .shp file extension. To overwrite an existing file, use delete_dsn=TRUE.

---

28. in Windows.↩︎

29. For a complete list of vector formats that can be read with st_read, run st_drivers(what='vector').↩︎